20151118:删除11种4阶环的内容。
20151026添加:
gap> LoadPackage("guava");
true
gap> q:=5;F:=GF(q);R:=PolynomialRing(F,2);;
5
GF(5)
gap> vars:=IndeterminatesOfPolynomialRing(R);x:=vars[1];y:=vars[2];
[ x_1, x_2 ]
x_1
x_2
gap> crv:=AffineCurve(y^3-x^3-x-1,R);
rec( polynomial := -x_1^3+x_2^3-x_1-Z(5)^0, ring := GF(5)[x_1,x_2] )
gap> g:=GenusCurve(crv);
1
gap> crv:=AffineCurve(y^2-x^3,R);
rec( polynomial := -x_1^3+x_2^2, ring := GF(5)[x_1,x_2] )
gap> g:=GenusCurve(crv);
1
定义在域F上的仿射代数曲线可以看作是F_n中由若干个n-元多项式定义的公共零点,使得其维数为一。
1.亏格为0的曲线:这种曲线至少有一个有理点在上面,在仿射或射影空间中,有理点是明显的或容易找到的。
2.亏格为1的曲线:这种曲线至少有一个可见的有理点和一个可见的有理对。
定理:设两三次曲线交9个点,如果第三条三次曲线过其中8个点,那么它一定过第九个点。
定理(2000):设两曲线Cm和Cn交mn个点,如果第三条曲线Cm+n-k过其中mn-(k-2)个点,那么它一定过剩下的k-2个点。
三次曲线的分类早在Newton那里就已经开始了,最后划分为72类。牛顿1707年证明在坐标变换下三次曲线有标准方程:y^2=x^3+ax^2+bx+c
椭圆曲线可以由Weierstrass的P-函数参数化:x=P(u), y=P´(u)
椭圆曲线上的群结构(点之间可定义加法):P+0=P;P+V=0;P+Q=Q+P;(P+Q)+R=P+(Q+R).
高观点下的初等数学3.(德国)克莱因
chap27从精确理论观点讨论平面几何
若一条曲线可以通过直尺机械产生,它就是代数曲线。
比代数曲线更为特殊的是有理曲线。
一般,我们把能嵌入到复射影空间的光滑复流形都称为代数流形。
L(D)-L(K-D)=degD-g+1
dim ker@-dim coker@=1-g
弄明白什么叫“除子”,才可以真正明白Riemann-Roch定理。Riemann-Roch定理的前身是Riemann不等式:dimF>=1+n-g,dimF是紧Riemann曲面M上的亚纯函数(由极点控制)集合F构成的向量空间的维数,g是M的亏格。1864年,Riemann的学生Roch在不等式的左边添加一项而使之成为如今的Riemann-Roch定理:dimF-dimD=1+n-g,dimD表示在每个极点处有不小于一阶零点的全纯微 分构成的向量空间的维数。 20151119添加:
Gauss超几何函数
For scalar a, b, and c, hypergeom([a,b],c,z) is the Gauss hypergeometric function 2F1(a,b;c;z).
>> doc hypergeom
>> y=hypergeom(1,1,1) y = 2.7183 >> y=hypergeom([1,1],1,1) y = NaN + Infi
chap4重要的组合数
4.1二项式系数
对于正整数n及非负整数k,n>=k,称二项式定理中的系数(n,k)=[n]_k/k!为二项式系数。
? binomial(5,2)
%3 = 10
4.3高斯二项式系数
对指定常数q及非负整数n,r,定义高斯二项式系数为
命题:Gauss二项式系数的组合意义是:q为素数幂时[n,r]是GF(q)上n维向量空间的r维子空间个数。
命题:[n,r]_q是q的r(n-r)次多项式,且lim[q->1][n,r]_q=(n,r)。此时称[n,r]_q是(n,r)的q模拟。
gap> LoadPackage("quagroup");
|
| QuaGroup
|
----------- A package for dealing with quantized enveloping algebras
|
| Willem de Graaf
| degraaf@science.unitn.it true
gap> GaussianBinomial( 5, 2, _q^2 );
q^12+q^8+2*q^4+2+2*q^-4+q^-8+q^-12
gap> GaussianBinomial( 5, 2, _q);
q^6+q^4+2*q^2+2+2*q^-2+q^-4+q^-6
gap> GaussianBinomial( 5, 0, _q);
1
gap> GaussianBinomial( 5, 6, _q);
0
gap> GaussianBinomial( 5, 3, _q);
q^6+q^4+2*q^2+2+2*q^-2+q^-4+q^-6
chap9波利亚计数理论
1937年,(匈牙利-美)波利亚(G.Polya,1887-1985)提出波利亚计数定理。
9.1作用在集合上的群
对群G的两个子群H1和H2,若存在g∈G使得gH1g^-1=H2,则称这两个子群是彼此共轭的。
对于x∈X,称X的子集θ(x)为x所在的轨(orbit)。X中的两元同轨关系是一种等价关系。轨θ(x)即是X在G作用下所划分成的等价类(或称传递集、可迁集、可迁类)。对于x∈X,称G_x为x的稳定核(stabilizer)。
称|G|为G的阶,|X|为G的度。
命题9.1.1:稳定核是G的子群,而同一轨中各元的稳定核是彼此共轭的。
命题9.1.2:对于x∈X,有|G|=|θ(x)|•|G_x|。
六面体群(阶为24)分别作用于立方体的顶点集(度为8)、棱集合(度为12)与面集合(度为6)时
X90表示绕X轴顺时针旋转90°,对应P1X90=P2;
y90表示绕Y轴逆时针旋转90°,对应y90P1=P2。
http://www.doc88/p-692153995466.html
gap> X90:=[[1,0,0],[0,0,1],[0,-1,0]];;y90:=[[0,0,-1],[0,1,0],[1,0,0]];;C4:=GroupWithGenerators([X90]);;IdGroup(C4);G:=GroupWithGenerators([X90,y90]);;IdGroup(G);
[ 4, 1 ]
[ 24, 12 ]
gap> G:=SymmetricGroup(4);;IdGroup(G);cl:=ConjugacyClasses(G);
[ 24, 12 ]
[ ()^G, (1,2)^G, (1,2)(3,4)^G, (1,2,3)^G, (1,2,3,4)^G ]
gap> len:=Size(cl);for i in [1..len] do Print(Size(cl[i]),","); od;Print("\n");for i in [1..len] do Print(IdGroup(Centralizer(cl[i])),","); od;
5
1,6,3,8,6,
[ 24, 12 ],[ 4, 2 ],[ 8, 3 ],[ 3, 1 ],[ 4, 1 ],
gap> for i in [1..len] do Print(Representative(cl[i]),",",Size(cl[i]),",",Size(Centralizer(cl[i])),",",Elements(Centralizer(cl[i])),"\n");od;
(),1,24,[ (), (3,4), (2,3), (2,3,4), (2,4,3), (2,4), (1,2), (1,2)(3,4), (1,2,3), (1,2,3,4), (1,2,4,3), (1,2,4),
(1,3,2), (1,3,4,2), (1,3), (1,3,4), (1,3)(2,4), (1,3,2,4), (1,4,3,2), (1,4,2), (1,4,3), (1,4), (1,4,2,3),
(1,4)(2,3) ]
(1,2),6,4,[ (), (3,4), (1,2), (1,2)(3,4) ]
(1,2)(3,4),3,8,[ (), (3,4), (1,2), (1,2)(3,4), (1,3)(2,4), (1,3,2,4), (1,4,2,3), (1,4)(2,3) ]
(1,2,3),8,3,[ (), (1,2,3), (1,3,2) ]
(1,2,3,4),6,4,[ (), (1,2,3,4), (1,3)(2,4), (1,4,3,2) ]
9.2有关的群的运算
9.3置换群的轮换指标
9.4伯恩赛德引理
作用在X上的置换群G称为可迁的(transitive),若G在X上作用的轨道仅一个。对于正整数k,作用在X上的置换群G称为k可迁 的,若对X上的任两个k排列,存在某g∈G,可使其一个变为另一个。k>=2时的可迁亦可统称为重可迁。对¥t<=k,若G是k可迁的,则G亦是t可迁的。故一般所称的k可迁,常指最大可迁值。若G是k可迁的,而单位元是G中唯一固定k个点的置换,则G称为恰k可迁的。恰1可迁群称为在X上正则。
命题9.4.3:当n>=3时,对称群S_n是n可迁的,而交代群A_n是(n-2)可迁的。
9.5波利亚计数定理
9.6圈形排列问题
9.7图的计数多项式
9.8波利亚定理的推广
9.9波利亚定理的应用 gap> for q in [2..6] do l5:=q^6*(q^6-1)*(q^2-1);L5:=SmallSimpleGroup(l5);Print(l5,",",L5,"\n");od;
12096,fail
4245696,G(2, 3)
251596800,G(2, 4)
5859000000,G2(5)
76185748800,fail
gap> for q in [2..2] do l6:=q^24*(q^12-1)*(q^8-1)*(q^6-1)*(q^2-1);L6:=SmallSimpleGroup(l6);Print(l6,",",L6,"\n");od;
3311126603366400,F4(2)
gap> LoadPackage("sonata");
#I You may wish to install the xgap package
#I and enjoy the graphic capabilities of SONATA. ___________________________________________________________________________
/ ___
|| / \ /\ Version 2.6
|| || || |\ | / \ /\ Erhard Aichinger
\___ || || |\\ | /____\_____________/__\ Franz Binder
\ || || | \\ | / \ || / \ Juergen Ecker
|| \___/ | \\ | / \ || / \ Peter Mayr
|| | \\| / \ || Christof Noebauer
\___/ | \| || System Of Nearrings And Their Applications
Info: http://www.algebra.uni-linz.ac.at/Sonata/ true
gap> A4:=AlternatingGroup(4);;IdGroup(A4);InnA4:=InnerAutomorphisms(A4);;IdGroup(Group(InnA4));
[ 12, 3 ]
[ 12, 3 ]
1955年,谢瓦莱找出了一类单群——被称为谢瓦莱群;
http://brauer.maths.qmul.ac.uk/Atlas/v3/exc/G24/
gap> g:=SmallSimpleGroup(6048);Order(g);IsSimpleGroup(g);Order(SU(3,3));Order(GU(3,3));
PSU(3,3)
6048
true
6048
24192
gap> g:=SmallSimpleGroup(4245696);Order(g);IsSimpleGroup(g);
G(2, 3)
4245696
true
gap> g:=SmallSimpleGroup(251596800);Order(g);IsSimpleGroup(g);
G(2, 4)
251596800
true
gap> g:=SmallSimpleGroup(5859000000);Order(g);IsSimpleGroup(g);
G2(5)
5859000000
true
gap> g:=SmallSimpleGroup(3311126603366400);Order(g);IsSimpleGroup(g);
F4(2)
3311126603366400
true
gap> LoadPackage("unipot");
/======================================================\
! !
! GAP Package UNIPOT 1.2 !
! (Computations with elements of unipotent !
! subgroups of Chevalley Groups) !
! !
! by Sergei Haller <Sergei.Haller@math.uni-giessen.de> !
! !
! see ??unipot !
\======================================================/
true
E_7(3)的幺幂子群是3^63阶群
gap> g:= UnipotChevSubGr("E",7,GF(3));Order(g);
<Unipotent subgroup of a Chevalley group of type E7 over GF(3)>
1144561273430837494885949696427
gap> G:=CyclicGroup(3^63);
<pc group of size 1144561273430837494885949696427 with 63 generators>
E_6(2)的幺幂子群是2^36阶群
gap> g:= UnipotChevSubGr("E",6,GF(2));Order(g);
<Unipotent subgroup of a Chevalley group of type E6 over GF(2)>
68719476736
gap> G:=CyclicGroup(214841575522005575270400);
<pc group of size 214841575522005575270400 with 51 generators>
gap> L:= SimpleLieAlgebra( "E", 6, GF(2) );
<Lie algebra of dimension 78 over GF(2)>
gap> Size(L);
302231454903657293676544
E_8(7)的幺幂子群是7^120阶群
gap> g:= UnipotChevSubGr("E",8,GF(7));Order(g);
<Unipotent subgroup of a Chevalley group of type E8 over GF(7)>
258086210989349276047917817413172383631691140276099547911280598425927853437317437263620645695945672001
20151012添加: 矩阵A的特征多项式为|xE-A|
gap> A:=[ [ 1, 0,0], [ 1,0, 1 ], [ 0,1, 0] ];y:=CharacteristicPolynomial(A);Factors(y);A1:=TransposedMat(A);y1:=CharacteristicPolynomial(A1);Factors(y1);
[ [ 1, 0, 0 ], [ 1, 0, 1 ], [ 0, 1, 0 ] ]
x_1^3-x_1^2-x_1+1
[ x_1-1, x_1-1, x_1+1 ]
[ [ 1, 1, 0 ], [ 0, 0, 1 ], [ 0, 1, 0 ] ]
x_1^3-x_1^2-x_1+1
[ x_1-1, x_1-1, x_1+1 ]
gap> A100:=A^100;
[ [ 1, 0, 0 ], [ 50, 1, 0 ], [ 50, 0, 1 ] ]
向量内积
gap> theta:=[2,0,-1];;t:=ScalarProduct(theta,theta);
5
gap> theta1:=[2,0,0,0,-1,-1];;t1:=ScalarProduct(theta1,theta1);
6
gap> theta1:=[2,0,0,0,-1,-1];;theta2:=[1,-1,-1,-1,1,1];;theta3:=[1,1,1,1,1,1];;t12:=ScalarProduct(theta1,theta2);t13:=ScalarProduct(theta1,theta3);t23:=ScalarProduct(theta2,theta3);
0
0
0
gap> theta:=[1,E(3),E(3)^2];;t:=ScalarProduct(theta,theta);
0
//线性卷积conv
//1.000000 6.000000 16.000000 26.000000 31.000000 20.000000
gap> a:=[1,2,3,4];;b:=[1,4,5];;ProductCoeffs(a,b);
[ 1, 6, 16, 26, 31, 20 ]
gap> lo:= LieObject( [ [ 1, 0 ], [ 0, 1 ] ] );m:=UnderlyingRingElement(lo);lo*lo;m*m;
LieObject( [ [ 1, 0 ], [ 0, 1 ] ] )
[ [ 1, 0 ], [ 0, 1 ] ]
LieObject( [ [ 0, 0 ], [ 0, 0 ] ] )
[ [ 1, 0 ], [ 0, 1 ] ]
三维叉积对加法的分配律,线性性和雅可比恒等式表明:具有向量加法和叉积的R^3构成了一个Lie代数。
a × (b × c) + b × (c × a) + c × (a × b) = 0
雅可比恒等式就是下列等式:[X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0
Lie代数是满足雅可比恒等式的代数结构的一个主要例子。
注意,满足雅可比恒等式的代数结构不一定满足反交换律。
x^3/6+x^2/2+x+1无有理根
2x^3-5x^2+5x-3的有理根为3/2
x^3-6x^2+15x-14的有理根为2
x^3/6+x^2/2+x+1无重根
x^3-3*x-2有重根
gap> x:=Indeterminate(Rationals);RootsOfUPol(x^3/6+x^2/2+x+1);
x_1
[ ]
gap> x:=Indeterminate(Rationals);RootsOfUPol(2*x^3-5*x^2+5*x-3);
x_1
[ 3/2 ]
gap> x:=Indeterminate(Rationals);RootsOfUPol(x^3-6*x^2+15*x-14);
x_1
[ 2 ]
gap> x:=Indeterminate(Rationals,"x");;y:=x^3/6+x^2/2+x+1;y1:=Derivative(y);Gcd(y,y1);GcdOp(y,y1);RootsOfUPol(y);
1/6*x^3+1/2*x^2+x+1
1/2*x^2+x+1
1
1
[ ]
gap> x:=Indeterminate(Rationals,"x");;y:=x^3-3*x-2;y1:=Derivative(y);Gcd(y,y1);GcdOp(y,y1);RootsOfUPol(y);
x^3-3*x-2
3*x^2-3
x+1
x+1
[ 2, -1, -1 ]
有理数域上的一元多项式环模不可约多项式生成的理想得到的无限域
gap> R:=PolynomialRing(Rationals,1);x:=Indeterminate(Rationals);poly:=x^2+x+1;IsIrreducibleRingElement(R,poly);Degree(poly);Factors(poly);F:=FieldByPolynomial(poly);Size(F);IsField(F);IsPrimeField(F);IsFinite(F);IsRationalsPolynomialRing(F);
Rationals[x_1]
x
x^2+x+1
true
2
[ x^2+x+1 ]
<algebraic extension over the Rationals of degree 2>
infinity
true
false
false
false
问题:GAP求基域为有理数域的可约多项式(例如f(x)=x^4-5*x^2+6=0)的伽罗瓦群?
注意:GAP软件中多项式环的功能尚不完善
R:=PolynomialRing(Rationals,1);IsUniqueFactorizationRing(R);IsIntegralRing(R);IsEuclideanRing(R);IsIrreducibleRingElement(R,x^2-2);IsIrreducibleRingElement(R,x^4-10*x^2+1);IsIrreducibleRingElement(R,50-45*x-6*x^2+x^3);IsIrreducibleRingElement(R,x^4-5*x^2+6);
R:=PolynomialRing(Rationals,2);IsUniqueFactorizationRing(R);IsEuclideanRing(R);
R:=PolynomialRing(Integers,1);IsUniqueFactorizationRing(R);IsEuclideanRing(R);
R:=PolynomialRing(Integers,2);IsUniqueFactorizationRing(R);IsEuclideanRing(R);
R:=PolynomialRing(GaussianIntegers,1);IsUniqueFactorizationRing(R);
R:=PolynomialRing(GaussianIntegers,2);IsUniqueFactorizationRing(R);
R:=PolynomialRing(GaussianRationals,1);IsUniqueFactorizationRing(R);IsIntegralRing(R);IsEuclideanRing(R);IsIrreducibleRingElement(R,x^2-2);
R:=PolynomialRing(GaussianRationals,2);IsUniqueFactorizationRing(R);IsEuclideanRing(R);
R:=UnivariatePolynomialRing(Rationals,"x");IsUniqueFactorizationRing(R);IsIntegralRing(R);IsIrreducibleRingElement(R,x^2-2);
R:=UnivariatePolynomialRing(Integers,"x");IsUniqueFactorizationRing(R);
R:=UnivariatePolynomialRing(GaussianRationals,"x");IsUniqueFactorizationRing(R);IsIntegralRing(R);IsIrreducibleRingElement(R,x^2-2);
R:=UnivariatePolynomialRing(GaussianIntegers,"x");IsUniqueFactorizationRing(R);
求方程x^3-2x-5=0的根。
gap> x:=Indeterminate(Rationals);RootsOfUPol(x^3-2*x-5);
x_1
[ ]
求方程x^3+2x^2+10x-20的根。
gap> x:=Indeterminate(Rationals);RootsOfUPol(x^3+2*x^2+10*x-20);
x_1
[ ]
gap> x:=Indeterminate(Rationals);RootsOfUPol(50-45*x-6*x^2+x^3);
x_1
[ 10, 1, -5 ]
gap> poly:=x^3-2*x-5;IsIrreducibleRingElement(PolynomialRing(Rationals,1),poly);IsSeparablePolynomial(poly);Degree(poly);
x^3-2*x-5
true
true
3
gap> poly:=x^3+2*x^2+10*x-20;IsIrreducibleRingElement(PolynomialRing(Rationals,1),poly);IsSeparablePolynomial(poly);Degree(poly);
x^3+2*x^2+10*x-20
true
true
3
gap> poly:=50-45*x-6*x^2+x^3;IsIrreducibleRingElement(PolynomialRing(Rationals,1),poly);IsSeparablePolynomial(poly);Degree(poly);
x^3-6*x^2-45*x+50
false
true
3
gap> poly:=x^4-5*x^2+6;IsIrreducibleRingElement(PolynomialRing(Rationals,1),poly);IsSeparablePolynomial(poly);Degree(poly);Factors(poly);
x^4-5*x^2+6
false
true
4
[ x^2-3, x^2-2 ]
定义:设F为域,称F[x]中多项式f(x)是F上的可分多项式,如果它在F[x]中的任一不可约因子都无重根(允许f(x)有重根)。否则,称f(x)是F上的不可分多项式。
任一无重根的不可约多项式必是可分多项式,不可分多项式的任一倍式必是不可分多项式。
完全域F上的多项式必是可分多项式。因为特征数为0的域和有限域必是完全域,因此,只有在特征数为p的无限域上才可能存在不可分多项式和不可分元。
gap> poly:=x^2+x+1;IsIrreducibleRingElement(PolynomialRing(GF(2),1),poly);Degree(poly);Factors(poly);
x^2+x+Z(2)^0
true
2
[ x^2+x+Z(2)^0 ]
gap> f:= MinimalPolynomial( Rationals, Sqrt(2) );
x^2-2
sqrt(2)在Q上的最小多项式为x^2-2。
gap> f:= MinimalPolynomial( Rationals, Sqrt(-1) );
x^2+1
gap> f:= MinimalPolynomial( Rationals, Sqrt(2)+Sqrt(3) );
x^4-10*x^2+1
sqrt(2)+sqrt(3)在Q上的最小多项式为f(x)=x^4-10x^2+1
http://www.gap-system/Manuals/pkg/MatricesForHomalg/doc/chap3.html
gap> LoadPackage("RingsForHomalg");
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading AutoDoc 2014.08.21 (Generate documentation from GAP source code)
by Sebastian Gutsche ( http://wwwb.math.rwth-aachen.de/~gutsche/) and
Max Horn ( http://www.quendi.de/math).
Homepage: http://wwwb.math.rwth-aachen.de/~gutsche/gap_packages/AutoDoc
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading ToolsForHomalg 2014.12.08 (Provides special methods and knowledge propagation tools)
by Mohamed Barakat ( http://www.mathematik.uni-kl.de/~barakat/),
Sebastian Gutsche ( http://wwwb.math.rwth-aachen.de/~gutsche/), and
Markus Lange-Hegermann ( http://wwwb.math.rwth-aachen.de/~markus/).
Homepage: http://wwwb.math.rwth-aachen.de/~gutsche/gap_packages/ToolsForHomalg
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading MatricesForHomalg 2015.02.03 (Lazy evaluated matrices with clever operations for the homalg project)
by Mohamed Barakat ( http://www.mathematik.uni-kl.de/~barakat/),
Markus Lange-Hegermann ( http://wwwb.math.rwth-aachen.de/~markus/),
Martin Leuner ( http://wwwb.math.rwth-aachen.de/Mitarbeiter/leuner.php), and
Vinay Wagh ( http://www.iitg.ernet.in/vinay.wagh/).
Homepage: http://homalg.math.rwth-aachen.de/index.php/core-packages/matricesforhomalg
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading HomalgToCAS 2015.02.03 (A window to the outer world)
by Thomas Bächler ( http://wwwb.math.rwth-aachen.de/~thomas/),
Mohamed Barakat ( http://www.mathematik.uni-kl.de/~barakat/),
Simon Görtzen ( http://wwwb.math.rwth-aachen.de/~simon/),
Sebastian Gutsche ( http://wwwb.math.rwth-aachen.de/~gutsche/), and
Vinay Wagh ( http://www.iitg.ernet.in/vinay.wagh/).
Homepage: http://homalg.math.rwth-aachen.de/index.php/core-packages/homalgtocas
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading RingsForHomalg 2015.02.10 (Dictionaries of external rings for the homalg project)
by Mohamed Barakat ( http://www.mathematik.uni-kl.de/~barakat/),
Simon Goertzen ( http://wwwb.math.rwth-aachen.de/goertzen/),
Markus Kirschmer ( http://www.math.rwth-aachen.de/~Markus.Kirschmer/),
Markus Lange-Hegermann ( http://wwwb.math.rwth-aachen.de/~markus/),
Oleksandr Motsak ( http://www.mathematik.uni-kl.de/~motsak/),
Daniel Robertz ( http://wwwb.math.rwth-aachen.de/~daniel/),
Hans Schönemann ( http://www.mathematik.uni-kl.de/~hannes/),
Andreas Steenpaß (), and
Vinay Wagh ( http://www.iitg.ernet.in/vinay.wagh/).
Homepage: http://homalg.math.rwth-aachen.de/index.php/core-packages/ringsforhomalg
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
true
gap> ZZ:=HomalgRingOfIntegers();
Z
gap> IsHomalgRing(ZZ);
true
gap> IsHomalgRing(Integers);
false
gap> IsPreHomalgRing(ZZ);
false
gap> IsPreHomalgRing(Integers);
false
gap> Display( ZZ );
<An internal ring>
gap> Z256 := ZZ / 2^8;
Z/( 256 )
gap> Display( Z256 );
<A residue class ring>
gap> Z2 := Z256 / 6;
Z/( 256, 6 )
gap> BasisOfRows( MatrixOfRelations( Z2 ) );
<An unevaluated non-zero 1 x 1 matrix over an internal ring>
gap> Z2;
Z/( 2 )
gap> Display( Z2 );
<A residue class ring>
gap> F2 := HomalgRingOfIntegers()/2;
Z/( 2 )
gap> Z6 := HomalgRingOfIntegers()/6;
Z/( 6 )
gap> Z4:= HomalgRingOfIntegers()/4;
Z/( 4 )
gap> IsZero(ZZ);
false
gap> ContainsAField(ZZ);ContainsAField(F2);
false
true
gap> IsRationalsForHomalg(ZZ);IsRationalsForHomalg(F2);
false
false
gap> IsFieldForHomalg(ZZ);IsFieldForHomalg(F2);IsFieldForHomalg(Z6);IsFieldForHomalg(Z4);
false
true
false
false
gap> IsDivisionRingForHomalg(ZZ);IsDivisionRingForHomalg(F2);IsDivisionRingForHomalg(Z6);
false
true
false
gap> IsResidueClassRingOfTheIntegers(ZZ);IsResidueClassRingOfTheIntegers(F2);IsResidueClassRingOfTheIntegers(Z6);IsResidueClassRingOfTheIntegers(Z4);
true
true
true
true
gap> IsBezoutRing(ZZ);
true
gap> IsIntegrallyClosedDomain(ZZ);
true
gap> IsUniqueFactorizationDomain(ZZ);IsUniqueFactorizationDomain(F2);
true
true
gap> IsKaplanskyHermite(ZZ);
true
gap> IsDedekindDomain(ZZ);IsDedekindDomain(F2);IsDedekindDomain(Z6);
true
true
false=>主理想环PIR和主理想整环PID是不同的
每个主理想整环PID都是戴德金整环。
代数数论(algebraic number theory)中的最基本事实是:
一个代数数域K中的代数整数全体(称为K的整数环)/满足理想唯一分解条件的整环是一个戴德金整环(Dedekind Domain)[是整数环Z的弱抽象,是整环的强抽象]。
每个理想可以唯一表示为素理想的乘积。
理想全体是素理想生成的乘法半群,其分式理想全体是一个乘法群,称为K的理想群。
正是这种“理想的唯一素分解”可部分弥补“复数一般不能唯一素因子分解”的不足,在历史上使代数数论发展起来。
理想的唯一分解定理:代数整数环中每一个非平凡理想都可以唯一分解为有限多个素理想的乘积。
gap> IsIntegralDomain(ZZ);IsIntegralDomain(F2);IsIntegralDomain(Z6);
true
true
false
gap> IsNoetherian(ZZ);IsNoetherian(F2);IsNoetherian(Z6);
true
true
true=>诺特环不一定要求是整环
交换代数中的希尔伯特基定理(1888年):若R为诺特环,则R[x]亦然。
[一个系数环上的任何多个变量的多项式所成的环,当这系数的环有一个单位元素和一组有限基时,这多项式环本身也有一组有限基。]
gap> IsLeftNoetherian(ZZ);IsLeftNoetherian(Z6);
true
true
gap> IsRightNoetherian(ZZ);IsRightNoetherian(Z6);
true
true
gap> IsArtinian(ZZ);IsArtinian(F2);
false
整数环是非阿廷环的诺特环
true
gap> IsLeftArtinian(ZZ);
false
gap> IsRightArtinian(ZZ);
false
gap> IsPrincipalIdealRing(ZZ);IsPrincipalIdealRing(F2);IsPrincipalIdealRing(Z6);
true
true
true
证明:整数环Z的每个理想都是主理想。
证明:模m剩余类环的每个理想都是主理想。=>主理想环PIR不一定要求是整环
gap> IsLeftPrincipalIdealRing(ZZ);
true
gap> IsRightPrincipalIdealRing(ZZ);
true
gap> IsRegular(ZZ);IsRegular(F2);
true
true
冯·诺伊曼引入的正则环(regular ring)->戴德金环
同调代数http://www.docin/p-67295980.html
gap> LoadPackage("RingsForHomalg");
true
gap> ZZ:=HomalgRingOfIntegers();
Z
gap> M := HomalgMatrix( "[ 2, 3, 4, 5, 6, 7 ]", 2, 3, ZZ );
<A 2 x 3 matrix over an internal ring>
gap> LoadPackage("Modules");
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading Modules 2015.02.10 (A homalg based package for the Abelian category of finitely presented modules over computable rings)
by Thomas Bächler (http://wwwb.math.rwth-aachen.de/~thomas/),
Mohamed Barakat (http://www.mathematik.uni-kl.de/~barakat/),
Florian Diebold (),
Sebastian Gutsche (http://wwwb.math.rwth-aachen.de/~gutsche/), and
Markus Lange-Hegermann (http://wwwb.math.rwth-aachen.de/~markus/).
Homepage: http://homalg.math.rwth-aachen.de/index.php/core-packages/modules
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
true
gap> M := LeftPresentation( M );
<A non-torsion left module presented by 2 relations for 3 generators>
gap> Display( M );
[ [ 2, 3, 4 ],
[ 5, 6, 7 ] ] Cokernel of the map Z^(1x2) --> Z^(1x3), currently represented by the above matrix
gap> N := TorsionObject( M );
<A cyclic torsion left module presented by yet unknown relations for a cyclic generator>
gap> iota := TorsionObjectEmb( M );
<A monomorphism of left modules>
gap> psi := Ext( 1, iota, N );
<A homomorphism of right modules>
gap> ByASmallerPresentation( psi );
<A non-zero homomorphism of right modules>
gap> Display( psi );
[ [ 2 ] ] the map is currently represented by the above 1 x 1 matrix
gap> extNN := Range( psi );
<A non-zero cyclic torsion right module on a cyclic generator satisfying 1 relation>
gap> IsIdenticalObj( extNN, Ext( 1, N, N ) );
true
gap> extMN := Source( psi );
<A non-zero cyclic torsion right module on a cyclic generator satisfying 1 relation>
gap> IsIdenticalObj( extMN, Ext( 1, M, N ) );
true
gap> Display( extNN );
Z/< 3 >
gap> Display( extMN );
Z/< 3 >
F:\hxh1\MathTool\有限群\G60
定理:13种60阶群与它们的群元阶的分布一一对应[ 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 ]
Group GAP4(60,1) [C5 x (C3 : C4)]1,1,2,6,4,2,4,0,8,24,8,0,
Group GAP4(60,2) [C3 x (C5 : C4)] 1,1,2,10,4,2,4,20,8,0,8,0,
Group GAP4(60,3) [C15 : C4] 1,1,2,30,4,2,4,0,8,0,8,0,
gap> IdGroup(QuaternionGroup(60));
[ 60, 3 ]
Group GAP4(60,4) [C60] 1,1,2,2,4,2,4,4,8,8,8,16,
gap> IdGroup(CyclicGroup(60));
[ 60, 4 ]
Group GAP4(60,5) [A5] 1,15,20,0,24,0,0,0,0,0,0,0,
60阶群PSL(2,5)同构于60阶群A_5。
GL(2,4)是(16-1)(16-4)=180阶群
GL(2,5)是(25-1)(25-5)=480阶群,SL(2,5)是480/4=120阶群,PSL(2,5)是120/2=60阶群。
gap> IdGroup(Group((1,2,3,4,5),(1,3,2)));
[ 60, 5 ]
gap> IdGroup(Group((1,2,3,4,5),(1,2)(3,4)));
[ 60, 5 ]
gap> IdGroup(Group((3,6)(4,5),(1,2,3)(4,6,5)));
[ 60, 5 ]
gap> IdGroup(Group((1,2)(3,4),(1,3,5)));
[ 60, 5 ]
gap> G:=SmallGroup(6,2);
<pc group of size 6 with 2 generators>
gap> i:=IsomorphismPermGroup(G);
[ f1, f2^2 ] -> [ (1,2), (3,4,5) ]
gap> Image(i,G);
Group([ (1,2), (3,4,5) ])
gap> Elements(Image(i,G));
[ (), (3,4,5), (3,5,4), (1,2), (1,2)(3,4,5), (1,2)(3,5,4) ]
Group GAP4(60,6) [C3 x (C5 : C4)] 1,5,2,10,4,10,0,20,8,0,0,0,
Group GAP4(60,7) [C15 : C4] 1,5,2,30,4,10,0,0,8,0,0,0,
Group GAP4(60,8) [S3 x D10] 1,23,2,0,4,10,12,0,8,0,0,0,
Group GAP4(60,9) [C5 x A4] 1,3,8,0,4,0,12,0,32,0,0,0,
Group GAP4(60,10) [C6 x D10] 1,11,2,0,4,22,4,0,8,0,8,0,
Group GAP4(60,11) [C10 x S3] 1,7,2,0,4,2,28,0,8,0,8,0,
gap> IdGroup(DirectProduct(CyclicGroup(10),SymmetricGroup(3)));
[ 60, 11 ]
Group GAP4(60,12) [D60] 1,31,2,0,4,2,4,0,8,0,8,0,
第13种60阶群:C_15×C_2×C_2
gap> G:=DirectProduct(CyclicGroup(30),CyclicGroup(2));IdGroup(G);L:=List(Elements(G),Order);M:=[1,2,3,4,5,6,10,12,15,20,30,60];for i in M do Print(Size(Positions(L,i)),","); od;
<pc group of size 60 with 4 generators>
[ 60, 13 ]
[ 1, 30, 15, 5, 2, 10, 30, 30, 15, 15, 30, 5, 10, 6, 10, 10, 30, 30, 3, 30, 15, 30, 5, 10, 30, 6, 2, 10, 30, 30, 15,
6, 3, 30, 5, 10, 30, 30, 10, 2, 6, 30, 15, 30, 15, 6, 10, 30, 30, 10, 10, 6, 15, 30, 30, 30, 30, 10, 30, 30 ]
[ 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 ]
1,3,2,0,4,6,12,0,8,0,24,0,
F:\hxh1\MathTool\有限群\G36
gap> IdGroup(QuaternionGroup(36));
[ 36, 1 ]
gap> IdGroup(Group((1,2,3,4,5,6,7,8,9),(10,11,12,13)));
[ 36, 2 ]
gap> IdGroup(Group((1,2,5)(7,8,9),(1,3,5)));
[ 36, 11 ]
gap> IdGroup(Group((3,5,14),(1,3)(2,6,8)(5,14)));
[ 36, 11 ]
gap> IdGroup(Group((1,2)(4,5),(3,5)(7,9,8)));
[ 36, 12 ]
gap> IdGroup(Group((2,8,6)(7,9),(1,3)(5,7,9)));
[ 36, 12 ]
gap> IdGroup(Group((2,8)(9,10,11),(1,6)(3,8)));
[ 36, 12 ]
gap> IdGroup(Group((2,8)(9,10,11),(1,5)(3,8)));
[ 36, 12 ]
gap> IdGroup(Group((2,8)(9,10,18),(1,5)(13,15,17)));
[ 36, 14 ]
F:\hxh1\MathTool\有限群\G24
定理:15种24阶群与它们的群元阶的分布一一对应[ 1, 2, 3, 4, 6, 8, 12, 24 ]
Group GAP4(24,1) [C3 : C8] 1,1,2,2,2,12,4,0,
Group GAP4(24,2) [C24] 1,1,2,2,2,4,4,8,
Group GAP4(24,3) [SL(2,3)] 1,1,8,6,8,0,0,0,
48个可逆的F_3上的2阶方阵构成一般线性群GL(2,3)。----SL(2,3)是24阶群,GL(2,3)是48阶群
GAP4[48,29]=GL(2,3)是(9-1)(9-3)=48阶群
Group GAP4(24,4) [C3 : Q8] 1,1,2,14,2,0,4,0,
gap> IdGroup(QuaternionGroup(24));
[ 24, 4 ]
Group GAP4(24,5) [C4 x S3] 1,7,2,8,2,0,4,0,
Group GAP4(24,6) [D24] 1,13,2,2,2,0,4,0,
Group GAP4(24,7) [C2 x (C3 : C4)] 1,3,2,12,6,0,0,0,
Group GAP4(24,8) [(C6 x C2) : C2] 1,9,2,6,6,0,0,0,
Group GAP4(24,9) [C12 x C2] 1,3,2,4,6,0,8,0,
Group GAP4(24,10) [C3 x D8] 1,5,2,2,10,0,4,0,
Group GAP4(24,11) [C3 x Q8] 1,1,2,6,2,0,12,0,
Group GAP4(24,12) [S4] 1,9,8,6,0,0,0,0,
Group GAP4(24,13) [C2 x A4] 1,7,8,0,8,0,0,0,
Group GAP4(24,14) [C2 x C2 x S3] 1,15,2,0,6,0,0,0,
Group GAP4(24,15) [C6 x C2 x C2]1,7,2,0,14,0,0,0,
gap> IdGroup(Group((1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24)));
[ 24, 2 ]
gap> IdGroup(Group((1,2,3)(4,6,5),(2,5,7)(3,8,6)));
[ 24, 3 ]
gap> IdGroup(Group((1,2,4,3)(5,6),(5,7)));
[ 24, 5 ]
gap> IdGroup(Group((2,3),(1,2)(5,6,7,8)));
[ 24, 5 ]
gap> IdGroup(Group((2,4)(6,7)(9,10),(1,2,3,4)(6,7)(8,9,10)(11,12)));
[ 24, 6 ]
gap> IdGroup(Group((2,4)(6,7)(9,10),(1,2)(3,4)(6,7,8)(11,12)));
[ 24, 8 ]
gap> IdGroup(Group((1,2,3,4),(1,4)(2,3)(5,6,7)));
[ 24, 10 ]
gap> IdGroup(SymmetricGroup(4));
[ 24, 12 ]
验证:S_4共有4!个元素,可由它的5个对换生成:
gap> IdGroup(SymmetricGroup(4))=Group((1,2),(1,3),(1,4),(2,4),(3,4));
true
gap> IdGroup(Group((1,2),(1,3),(1,4),(2,4),(3,4)));
[ 24, 12 ]
gap> IdGroup(Group((2,4,3),(1,2,3,4)));
[ 24, 12 ]
gap> IdGroup(Group((1,2,3,5),(2,3)));
[ 24, 12 ]
gap> IdGroup(Group((4,5),(2,3,4)));
[ 24, 12 ]
gap> IdGroup(Group((1,4,6,5),(1,3,4)(2,5,6)));
[ 24, 12 ]
gap> IdGroup(Group((1,7,4,10),(1,10)));
[ 24, 12 ]
gap> IdGroup(Group((1,6,4,2,5,3),(5,6)));
[ 24, 13 ]
gap> IdGroup(Group((1,5)(3,8,9,4,6,10),(1,5)(9,10)));
[ 24, 13 ]
F:\hxh1\MathTool\有限群\G4
gap> IdGroup(Group((1,2,3,4)));
[ 4, 1 ]
gap> IdGroup(Group((3,4),(1,2)));
[ 4, 2 ]
F:\hxh1\MathTool\有限群\G6
gap> IdGroup(Group((2,4),(4,5)));
[ 6, 1 ]
gap> IdGroup(Group((1,2,3),(5,6)(7,8)(9,10)));
[ 6, 2 ]
gap> IdGroup(Group((1,2,3,4,5,6)));
[ 6, 2 ]
F:\hxh1\MathTool\有限群\G8
gap> IdGroup(Group((1,2),(3,4,5,6)));
[ 8, 2 ]
gap> IdGroup(Group((1,2,3,4),(5,6)));
[ 8, 2 ]
gap> IdGroup(Group((1,2,3,4),(5,6),(1,3)(2,4),(1,3)(2,4)(5,6),(1,4,3,2),(1,4,3,2)(5,6),(1,2,3,4)(5,6)));
[ 8, 2 ]
gap> IdGroup(Group((1,2,3,4),(1,4,3,2)(5,7)(6,8)));
[ 8, 2 ]
gap> IdGroup(Group((1,2)(3,4)(5,6)(7,8),(1,5,2,6)(3,7,4,8),(1,7,2,8)(3,5,4,6)));
[ 8, 2 ]
gap> IdGroup(Group((1,2,3,4),(1,3)));
[ 8, 3 ]
gap> IdGroup(Group((1,2,3,4),(2,4)(5,6)));
[ 8, 3 ]
gap> IdGroup(Group((1,3)(2,4)(6,7),(2,3)));
[ 8, 3 ]
gap> IdGroup(Group((2,4)(6,7)(9,10),(1,2,3,4)(6,7)(11,12)));
[ 8, 3 ]F:\hxh1\MathTool\有限群\G9
gap> IdGroup(Group((1,2,3),(4,5,6)));
[ 9, 2 ]
gap> IdGroup(Group((1,2,3),(4,5,6),(1,3,2),(4,6,5),(1,2,3)(4,5,6),(1,2,3)(4,6,5),(1,3,2)(4,6,5),(1,3,2)(4,5,6)));
[ 9, 2 ]
F:\hxh1\MathTool\有限群\G12
gap> IdGroup(Group((1,6)(4,5),(1,2,6,5,3,4)));
[ 12, 4 ]
gap> IdGroup(Group((1,3,5)(4,6),(1,5)));
[ 12, 4 ]
F:\hxh1\MathTool\有限群\Sn的子群
gap> G:=SmallGroup(8,1);
<pc group of size 8 with 3 generators>
gap> i:=IsomorphismPermGroup(G);
[ f1*f2 ] -> [ (1,2,3,4,5,6,7,8) ]
gap> Image(i,G);
Group([ (1,2,3,4,5,6,7,8) ])
gap> Elements(Image(i,G));
[ (), (1,2,3,4,5,6,7,8), (1,3,5,7)(2,4,6,8), (1,4,7,2,5,8,3,6), (1,5)(2,6)(3,7)(4,8), (1,6,3,8,5,2,7,4),
(1,7,5,3)(2,8,6,4), (1,8,7,6,5,4,3,2) ]
gap> IdGroup(Group((1,2,3,4,5,6,7,8)));
[ 8, 1 ]
gap> IdGroup(Group((1,5,3,7,2,6,4,8),(1,3,2,4)(5,7,6,8),(1,2)(3,4)(5,6)(7,8)));
[ 8, 1 ]
gap> IdGroup(Group((1,2),(3,4,5,6)));
[ 8, 2 ]
gap> IdGroup(Group((2,4)(6,7)(9,10),(1,2,3,4)(6,7)(11,12)));
gap> IdGroup(DihedralGroup(8));
[ 8, 3 ]
gap> IdGroup(DihedralGroup(IsPermGroup,8));
Group([(1,2,3,4),(2,4)])
[ 8, 3 ]
gap> IdGroup(Group((1,3)(2,4),(1,4)(2,3),(3,4)));
[ 8, 3 ]
gap> IdGroup(Group((1,5,2,6)(3,8,4,7),(1,3,2,4)(5,7,6,8),(1,2)(3,4)(5,6)(7,8)));
[ 8, 4 ]
gap> IdGroup(QuaternionGroup(8));
[ 8, 4 ]
gap> IdGroup(ElementaryAbelianGroup(8));
[ 8, 5 ]
gap> IdGroup(Group((1,2),(3,4),(5,6)));
[ 8, 5 ]
gap> IdGroup(Group((1,2),(3,4),(5,6),(1,2)(3,4),(1,2)(5,6),(3,4)(5,6),(1,2)(3,4)(5,6)));
[ 8, 5 ]
gap> IdGroup(Group((1,2,3)(4,5),(4,5)(7,8)));
[ 12, 5 ]
gap> IdGroup(Group((1,2,3)(4,5)(6,7),(1,3,2)(6,7)));
[ 12, 5 ]
gap> IdGroup(Group((1,2,3)(4,5)(6,7),(1,3,2)(6,7),(1,3,2)));
[ 12, 5 ]
gap> IdGroup(Group((1,2,3,4,5,6)(7,8,9,10,11,12),(1,7,4,10)(2,12,5,9)(3,11,6,8)));
[ 12, 1 ]
gap> IdGroup(Group((1,2,3,4,5,6)(7,8,9,10,11,12),(1,7,4,10)(2,12,5,9)(3,11,6,8),(1,6,5,4,3,2)(7,12,11,10,9,8),(1,3,5)(2,4,6)(7,9,11)(8,10,12),(1,4)(2,5)(3,6)(7,10)(8,11)(9,12)));
[ 12, 1 ]
gap> IdGroup(QuaternionGroup(12));
[ 12, 1 ]
gap> IdGroup(Group((1,2,3,4,5,6,7,8,9,10,11,12)));
[ 12, 2 ]
gap> IdGroup(Group((),(1,2,3),(1,3,2),(1,2,4),(1,4,2),(1,3,4),(1,4,3),(2,3,4),(2,4,3),(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)));
[ 12, 3 ]
gap> IdGroup(Group((5,6),(1,2,3)(4,5)));
[ 18, 3 ]
gap> IdGroup(Group((3,6)(4,5),(2,4,5),(1,3)(4,5)));
[ 18, 4 ]
gap> IdGroup(QuaternionGroup(20));
[ 20, 1 ]
gap> IdGroup(Group((2,3)(4,5),(1,2,3,4)));
[ 20, 3 ]
http://groupprops.subwiki/wiki/GAP:IdGroup
gap> IdGroup(CyclicGroup(6));
[ 6, 2 ]
gap> IdGroup(SL(2,5));
[ 120, 5 ]
gap> IdGroup(SL(2,5))[2];
5
gap> IdGroup(SmallGroup(24,7));
[ 24, 7 ]
gap> G := SymmetricGroup(4);
Sym( [ 1 .. 4 ] )
gap> H := DirectProduct(G,G);
Group([ (1,2,3,4), (1,2), (5,6,7,8), (5,6) ])
gap> IdGroup(H);
[ 576, 8653 ]
gap> G:=SmallGroup(6,2);
<pc group of size 6 with 2 generators>
gap> List(NormalSubgroups(G),IdGroup);
[ [ 6, 2 ], [ 2, 1 ], [ 3, 1 ], [ 1, 1 ] ]
gap> V4:=Group([(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)]);
Group([ (1,2)(3,4), (1,3)(2,4), (1,4)(2,3) ])
gap> IdGroup(V4);
[ 4, 2 ]
群的置换表示和GAP ID
3,9,12,13?
gap> IdGroup(Group([(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16)]));[ 16, 1 ]
gap> IdGroup(Group([(1,2,3,4),(5,6,7,8)]));[ 16, 2 ]
gap> IdGroup(Group((1,7,4,10),(5,6,8,9)));
[ 16, 2 ]
gap> IdGroup(Group([(1,2,3,4),(1,3)(5,6,7,8)]));[ 16, 4 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(9,10)]));[ 16, 5 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(1,5)(3,7)]));[ 16, 6 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(1,7)(3,5)(2,6)]));[ 16, 7 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(1,3)(5,7)(2,6)]));[ 16, 8 ]
gap> IdGroup(Group([(1,2,3,4),(5,6),(7,8)]));[ 16, 10 ]
gap> IdGroup(Group([(1,2,3,4),(1,3),(5,6)]));[ 16, 11 ]
gap> IdGroup(Group([(1,2),(3,4),(5,6),(7,8)]));[ 16, 14 ]
gap> IdGroup(ElementaryAbelianGroup(16));
[ 16, 14 ]
gap> IdGroup(Group((1,5)(2,6)(3,4,8,9)(7,10),(1,6)));
[ 16, 3 ]
两个生成元分别是4阶元和2阶元
gap> G:=SmallGroup(16,3);
<pc group of size 16 with 4 generators>
gap> i:=IsomorphismPermGroup(G);
<action isomorphism>
gap> Image(i,G);
Group([ (1,2,5,8)(3,12,10,16)(4,7,11,14)(6,15,13,9), (1,3)(2,6)(4,9)(5,10)(7,12)(8,13)(11,15)(14,16), (1,4)(2,7)(3,9)
(5,11)(6,12)(8,14)(10,15)(13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16) ])
gap> Elements(Image(i,G));
[ (), (1,2,5,8)(3,12,10,16)(4,7,11,14)(6,15,13,9), (1,3)(2,6)(4,9)(5,10)(7,12)(8,13)(11,15)(14,16),
(1,4)(2,7)(3,9)(5,11)(6,12)(8,14)(10,15)(13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16),
(1,6,11,16)(2,10,14,9)(3,7,15,8)(4,12,5,13), (1,7,5,14)(2,11,8,4)(3,6,10,13)(9,12,15,16),
(1,8,5,2)(3,16,10,12)(4,14,11,7)(6,9,13,15), (1,9)(2,12)(3,4)(5,15)(6,7)(8,16)(10,11)(13,14),
(1,10)(2,13)(3,5)(4,15)(6,8)(7,16)(9,11)(12,14), (1,11)(2,14)(3,15)(4,5)(6,16)(7,8)(9,10)(12,13),
(1,12,11,13)(2,15,14,3)(4,6,5,16)(7,10,8,9), (1,13,11,12)(2,3,14,15)(4,16,5,6)(7,9,8,10),
(1,14,5,7)(2,4,8,11)(3,13,10,6)(9,16,15,12), (1,15)(2,16)(3,11)(4,10)(5,9)(6,14)(7,13)(8,12),
(1,16,11,6)(2,9,14,10)(3,8,15,7)(4,13,5,12) ]
gap> IdGroup(QuaternionGroup(16));
[ 16, 9 ]
gap> G:=SmallGroup(16,9);
<pc group of size 16 with 4 generators>
gap> i:=IsomorphismPermGroup(G);
<action isomorphism>
gap> Image(i,G);
Group([ (1,2,5,8)(3,12,10,16)(4,14,11,7)(6,15,13,9), (1,3,5,10)(2,6,8,13)(4,15,11,9)(7,16,14,12), (1,4,5,11)(2,7,8,14)
(3,9,10,15)(6,12,13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16) ])
gap> Elements(Image(i,G));
[ (), (1,2,5,8)(3,12,10,16)(4,14,11,7)(6,15,13,9), (1,3,5,10)(2,6,8,13)(4,15,11,9)(7,16,14,12),
(1,4,5,11)(2,7,8,14)(3,9,10,15)(6,12,13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16),
(1,6,11,16,5,13,4,12)(2,10,14,9,8,3,7,15), (1,7,5,14)(2,11,8,4)(3,13,10,6)(9,12,15,16),
(1,8,5,2)(3,16,10,12)(4,7,11,14)(6,9,13,15), (1,9,5,15)(2,12,8,16)(3,11,10,4)(6,14,13,7),
(1,10,5,3)(2,13,8,6)(4,9,11,15)(7,12,14,16), (1,11,5,4)(2,14,8,7)(3,15,10,9)(6,16,13,12),
(1,12,4,13,5,16,11,6)(2,15,7,3,8,9,14,10), (1,13,11,12,5,6,4,16)(2,3,14,15,8,10,7,9),
(1,14,5,7)(2,4,8,11)(3,6,10,13)(9,16,15,12), (1,15,5,9)(2,16,8,12)(3,4,10,11)(6,7,13,14),
(1,16,4,6,5,12,11,13)(2,9,7,10,8,15,14,3) ]
gap> G:=SmallGroup(16,12);
<pc group of size 16 with 4 generators>
gap> i:=IsomorphismPermGroup(G);
<action isomorphism>
gap> Image(i,G);
Group([ (1,2,5,8)(3,13,10,6)(4,7,11,14)(9,16,15,12), (1,3,5,10)(2,6,8,13)(4,9,11,15)(7,12,14,16), (1,4)(2,7)(3,9)
(5,11)(6,12)(8,14)(10,15)(13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16) ])
gap> Elements(Image(i,G));
[ (), (1,2,5,8)(3,13,10,6)(4,7,11,14)(9,16,15,12), (1,3,5,10)(2,6,8,13)(4,9,11,15)(7,12,14,16),
(1,4)(2,7)(3,9)(5,11)(6,12)(8,14)(10,15)(13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16),
(1,6,5,13)(2,10,8,3)(4,12,11,16)(7,15,14,9), (1,7,5,14)(2,11,8,4)(3,16,10,12)(6,9,13,15),
(1,8,5,2)(3,6,10,13)(4,14,11,7)(9,12,15,16), (1,9,5,15)(2,12,8,16)(3,11,10,4)(6,14,13,7),
(1,10,5,3)(2,13,8,6)(4,15,11,9)(7,16,14,12), (1,11)(2,14)(3,15)(4,5)(6,16)(7,8)(9,10)(12,13),
(1,12,5,16)(2,15,8,9)(3,7,10,14)(4,6,11,13), (1,13,5,6)(2,3,8,10)(4,16,11,12)(7,9,14,15),
(1,14,5,7)(2,4,8,11)(3,12,10,16)(6,15,13,9), (1,15,5,9)(2,16,8,12)(3,4,10,11)(6,7,13,14),
(1,16,5,12)(2,9,8,15)(3,14,10,7)(4,13,11,6) ]
gap> G:=SmallGroup(16,13);
<pc group of size 16 with 4 generators>
gap> i:=IsomorphismPermGroup(G);
<action isomorphism>
gap> Image(i,G);
Group([ (1,2)(3,13)(4,7)(5,8)(6,10)(9,16)(11,14)(12,15), (1,3)(2,6)(4,9)(5,10)(7,12)(8,13)(11,15)(14,16), (1,4,5,11)
(2,7,8,14)(3,9,10,15)(6,12,13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16) ])
gap> Elements(Image(i,G));
[ (), (1,2)(3,13)(4,7)(5,8)(6,10)(9,16)(11,14)(12,15), (1,3)(2,6)(4,9)(5,10)(7,12)(8,13)(11,15)(14,16),
(1,4,5,11)(2,7,8,14)(3,9,10,15)(6,12,13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16),
(1,6,5,13)(2,3,8,10)(4,12,11,16)(7,9,14,15), (1,7,5,14)(2,4,8,11)(3,16,10,12)(6,15,13,9),
(1,8)(2,5)(3,6)(4,14)(7,11)(9,12)(10,13)(15,16), (1,9,5,15)(2,12,8,16)(3,4,10,11)(6,7,13,14),
(1,10)(2,13)(3,5)(4,15)(6,8)(7,16)(9,11)(12,14), (1,11,5,4)(2,14,8,7)(3,15,10,9)(6,16,13,12),
(1,12)(2,9)(3,14)(4,13)(5,16)(6,11)(7,10)(8,15), (1,13,5,6)(2,10,8,3)(4,16,11,12)(7,15,14,9),
(1,14,5,7)(2,11,8,4)(3,12,10,16)(6,9,13,15), (1,15,5,9)(2,16,8,12)(3,11,10,4)(6,14,13,7),
(1,16)(2,15)(3,7)(4,6)(5,12)(8,9)(10,14)(11,13) ]
S_4、S_5的子群
http://www.docin/p-670969262.html
董井成:GAP在近世代数教学中的应用
GAP是一款绿色软件,不需要安装,双击C:\gap4r7\bin下的批处理文件gap.bat即可启动软件,显示输入提示符gap>
。GAP的界面类似DOS。GAP语句以分号结尾,不能省略。
群的最高阶可以达到几万。
循环群、对称群、二面体群分别用函数
gap> IdGroup(CyclicGroup(3));
[ 3, 1 ]
gap> IdGroup(Group((1,2,3),(1,2,4),(1,3,4)));
[ 12, 3 ]
gap>IdGroup(Group((1,2,3),(1,3,2),(1,2,4),(1,4,2),(1,3,4),(1,4,3),(2,3,4),(2,4,3),(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)));
[ 12, 3 ]
偶置换:逆序数的个数是偶数。
奇置换:逆序数的个数是奇数。
(1)=(2)=(3)=(4)=I
8个长度3的轮换:(123),(124),(134)
长度4的轮换:
2个对换的乘积:
20151008:半直积的例子
gap> C3:=CyclicGroup(IsPermGroup,3);;C7:=CyclicGroup(IsPermGroup,7);;A:=AutomorphismGroup(C7);;elts := Elements(A);sigma := elts[4];sigma^3;map := GroupHomomorphismByImages(C3, A, GeneratorsOfGroup(C3), [sigma]);SDP := SemidirectProduct(C3, map, C7);IdGroup(SDP);List(elts,Order);IdGroup(DirectProduct( C3, C7 ));
[ [ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ], [ (1,2,3,4,5,6,7) ] -> [ (1,3,5,7,2,4,6) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,4,7,3,6,2,5) ], [ (1,2,3,4,5,6,7) ] -> [ (1,5,2,6,3,7,4) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,6,4,2,7,5,3) ], [ (1,2,3,4,5,6,7) ] -> [ (1,7,6,5,4,3,2) ] ]
[ (1,2,3,4,5,6,7) ] -> [ (1,5,2,6,3,7,4) ]
[ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ]
[ (1,2,3) ] -> [ [ (1,2,3,4,5,6,7) ] -> [ (1,5,2,6,3,7,4) ] ]
Group([ (4,5,6,7,8,9,10), (1,2,3)(5,8,6)(7,9,10) ])
[ 21, 1 ]
[ 1, 3, 6, 3, 6, 2 ]
[ 21, 2 ]
gap> C3:=CyclicGroup(IsPermGroup,3);;C7:=CyclicGroup(IsPermGroup,7);;A:=AutomorphismGroup(C7);;elts := Elements(A);sigma := elts[2];sigma^3;map := GroupHomomorphismByImages(C3, A, GeneratorsOfGroup(C3), [sigma]);SDP := SemidirectProduct(C3, map, C7);IdGroup(SDP);List(elts,Order);IdGroup(DirectProduct( C3, C7 ));
[ [ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ], [ (1,2,3,4,5,6,7) ] -> [ (1,3,5,7,2,4,6) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,4,7,3,6,2,5) ], [ (1,2,3,4,5,6,7) ] -> [ (1,5,2,6,3,7,4) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,6,4,2,7,5,3) ], [ (1,2,3,4,5,6,7) ] -> [ (1,7,6,5,4,3,2) ] ]
[ (1,2,3,4,5,6,7) ] -> [ (1,3,5,7,2,4,6) ]
[ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ]
[ (1,2,3) ] -> [ [ (1,2,3,4,5,6,7) ] -> [ (1,3,5,7,2,4,6) ] ]
Group([ (4,5,6,7,8,9,10), (1,2,3)(5,6,8)(7,10,9) ])
[ 21, 1 ]
[ 1, 3, 6, 3, 6, 2 ]
[ 21, 2 ]
gap> C3:=CyclicGroup(IsPermGroup,3);;C7:=CyclicGroup(IsPermGroup,7);;A:=AutomorphismGroup(C7);;elts := Elements(A);sigma := elts[1];sigma^3;map := GroupHomomorphismByImages(C3, A, GeneratorsOfGroup(C3), [sigma]);SDP := SemidirectProduct(C3, map, C7);IdGroup(SDP);List(elts,Order);IdGroup(DirectProduct( C3, C7 ));
[ [ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ], [ (1,2,3,4,5,6,7) ] -> [ (1,3,5,7,2,4,6) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,4,7,3,6,2,5) ], [ (1,2,3,4,5,6,7) ] -> [ (1,5,2,6,3,7,4) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,6,4,2,7,5,3) ], [ (1,2,3,4,5,6,7) ] -> [ (1,7,6,5,4,3,2) ] ]
[ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ]
[ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ]
[ (1,2,3) ] -> [ [ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ] ]
Group([ (4,5,6,7,8,9,10), (1,2,3) ])
[ 21, 2 ]
[ 1, 3, 6, 3, 6, 2 ]
[ 21, 2 ]
gap> C8:=CyclicGroup(IsPermGroup,8);;C3:=CyclicGroup(IsPermGroup,3);;A:=AutomorphismGroup(C3);;elts := Elements(A);sigma := elts[1];sigma^2;map := GroupHomomorphismByImages(C8, A, GeneratorsOfGroup(C8), [sigma]);SDP := SemidirectProduct(C8, map, C3);IdGroup(SDP);List(elts,Order);IdGroup(DirectProduct( C8, C3 ));
[ [ (1,2,3) ] -> [ (1,2,3) ], [ (1,2,3) ] -> [ (1,3,2) ] ]
[ (1,2,3) ] -> [ (1,2,3) ]
[ (1,2,3) ] -> [ (1,2,3) ]
[ (1,2,3,4,5,6,7,8) ] -> [ [ (1,2,3) ] -> [ (1,2,3) ] ]
Group([ (9,10,11), (1,2,3,4,5,6,7,8) ])
[ 24, 2 ]
[ 1, 2 ]
[ 24, 2 ]
gap> C8:=CyclicGroup(IsPermGroup,8);;C3:=CyclicGroup(IsPermGroup,3);;A:=AutomorphismGroup(C3);;elts := Elements(A);sigma := elts[2];sigma^2;map := GroupHomomorphismByImages(C8, A, GeneratorsOfGroup(C8), [sigma]);SDP := SemidirectProduct(C8, map, C3);IdGroup(SDP);List(elts,Order);IdGroup(DirectProduct( C8, C3 ));
[ [ (1,2,3) ] -> [ (1,2,3) ], [ (1,2,3) ] -> [ (1,3,2) ] ]
[ (1,2,3) ] -> [ (1,3,2) ]
[ (1,2,3) ] -> [ (1,2,3) ]
[ (1,2,3,4,5,6,7,8) ] -> [ [ (1,2,3) ] -> [ (1,3,2) ] ]
Group([ (9,10,11), (1,2,3,4,5,6,7,8)(10,11) ])
[ 24, 1 ]
[ 1, 2 ]
[ 24, 2 ]
20151006:GAP求有限群的共轭类个数以及每个共轭类的长度
gap> G:=SymmetricGroup(4);IdGroup(G);cl:=ConjugacyClasses(G);len:=Size(cl);for i in [1..len] do Print(Size(cl[i]),","); od;Print("\n");for i in [1..len] do Print(IdGroup(Centralizer(cl[i])),","); od;
Sym( [ 1 .. 4 ] )
[ 24, 12 ]
[ ()^G, (1,2)^G, (1,2)(3,4)^G, (1,2,3)^G, (1,2,3,4)^G ]
5
1,6,3,8,6,
[ 24, 12 ],[ 4, 2 ],[ 8, 3 ],[ 3, 1 ],[ 4, 1 ],
gap> G:=SmallGroup(48,11);IdGroup(G);L:=List(ConjugacyClasses(G),Size);len:=Size(L);M:=[1, 2, 3, 4, 6, 8, 12, 16, 24, 48];for i in M do Print(Size(Positions(L,i)),","); od;
<pc group of size 48 with 5 generators>
[ 48, 11 ]
[ 1, 3, 1, 1, 1, 2, 3, 3, 3, 1, 1, 2, 1, 2, 2, 3, 3, 3, 1, 2, 2, 2, 3, 2 ]
24
[ 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 ]
8,8,8,0,0,0,0,0,0,0,
gap> G:=SmallGroup(48,12);IdGroup(G);L:=List(ConjugacyClasses(G),Size);len:=Size(L);M:=[1, 2, 3, 4, 6, 8, 12, 16, 24, 48];for i in M do Print(Size(Positions(L,i)),","); od;
<pc group of size 48 with 5 generators>
[ 48, 12 ]
[ 1, 6, 2, 1, 1, 2, 6, 6, 2, 2, 1, 2, 2, 6, 2, 2, 2, 2 ]
18
[ 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 ]
4,10,0,0,4,0,0,0,0,0,
gap> G:=SmallGroup(48,13);IdGroup(G);L:=List(ConjugacyClasses(G),Size);len:=Size(L);M:=[1, 2, 3, 4, 6, 8, 12, 16, 24, 48];for i in M do Print(Size(Positions(L,i)),","); od;
<pc group of size 48 with 5 generators>
[ 48, 13 ]
[ 1, 6, 2, 1, 1, 2, 6, 6, 2, 2, 1, 2, 2, 6, 2, 2, 2, 2 ]
18
[ 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 ]
4,10,0,0,4,0,0,0,0,0,
gap> G:=SmallGroup(48,34);IdGroup(G);L:=List(ConjugacyClasses(G),Size);len:=Size(L);M:=[1, 2, 3, 4, 6, 8, 12, 16, 24, 48];for i in M do Print(Size(Positions(L,i)),","); od;
<pc group of size 48 with 5 generators>
[ 48, 34 ]
[ 1, 6, 1, 2, 1, 2, 6, 6, 2, 1, 2, 2, 2, 6, 2, 2, 2, 2 ]
18
[ 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 ]
4,10,0,0,4,0,0,0,0,0,
德国数学家弗罗贝尼乌斯(Ferdinand Georg Frobenius,1849.10.26-1917.8.3)曾经提出了一个著名的猜想:共轭类数为n的有限群,在同构意义下是有限的。该猜想最先由E.Landau证明,他给出了具有n个共轭类的有限群的阶的上界,从而肯定了猜想的正确性。
定理(Frobenius猜想):共轭类数为n的有限群,在同构意义下是有限的。
定理:有限群为交换群的充要条件是Con(G)=|G|。
定理:共轭类数为1的有限群,只能是单位元群C_1。共轭类数为2的有限群,只能是2阶循环群C_2。共轭类数为3的有限群,是可解群,是3阶循环群或者6阶群。
gap> Size(ConjugacyClasses(SmallGroup(6,1)));
3
gap> Size(ConjugacyClasses(SmallGroup(6,2)));
6
gap> Size(ConjugacyClasses(SmallGroup(1,1)));
1
gap> Size(ConjugacyClasses(SmallGroup(2,1)));
2
gap> Size(ConjugacyClasses(SmallGroup(3,1)));
3
gap> Size(ConjugacyClasses(SmallGroup(4,1)));
4
gap> Size(ConjugacyClasses(SmallGroup(4,2)));
4
gap> Size(ConjugacyClasses(SmallGroup(5,1)));
5
gap> Size(ConjugacyClasses(SmallGroup(48,11)));
24
gap> Size(ConjugacyClasses(SmallGroup(48,12)));
18
gap> Size(ConjugacyClasses(SmallGroup(48,13)));
18
gap> Size(ConjugacyClasses(SmallGroup(48,34)));
18
gap> IdGroup(AutomorphismGroup(SmallGroup(48,34)));
[ 384, 12882 ]
gap> IdGroup(AutomorphismGroup(SmallGroup(48,11)));
[ 192, 1147 ]
gap> IdGroup(AutomorphismGroup(SmallGroup(48,12)));
[ 96, 230 ]
gap> IdGroup(AutomorphismGroup(SmallGroup(48,13)));
[ 192, 1147 ]
gap> IsNilpotentGroup(SmallGroup(48,12));
false
gap> IsNilpotentGroup(SmallGroup(48,11));
false
gap> IsNilpotentGroup(SmallGroup(48,13));
false
gap> IsNilpotentGroup(SmallGroup(48,34));
false
gap> IsSolvableGroup(SmallGroup(48,12));
true
gap> IsSolvableGroup(SmallGroup(48,11));
true
gap> IsSolvableGroup(SmallGroup(48,13));
true
gap> IsSolvableGroup(SmallGroup(48,34));
true
gap> IsSupersolvableGroup(SmallGroup(48,34));
true
gap> IsSupersolvableGroup(SmallGroup(48,11));
true
gap> IsSupersolvableGroup(SmallGroup(48,12));
true
gap> IsSupersolvableGroup(SmallGroup(48,13));
true
gap> IsAlmostSimpleGroup(SmallGroup(48,13));
false
gap> IsAlmostSimpleGroup(SmallGroup(48,11));
false
gap> IsAlmostSimpleGroup(SmallGroup(48,12));
false
gap> IsAlmostSimpleGroup(SmallGroup(48,34));
false
gap> IsPolycyclicGroup(SmallGroup(48,34));
true
gap> IsPolycyclicGroup(SmallGroup(48,11));
true
gap> IsPolycyclicGroup(SmallGroup(48,12));
true
gap> IsPolycyclicGroup(SmallGroup(48,13));
true
20151003:GAP中计算多项式的伽罗瓦群:
gap> x:=Indeterminate(Rationals);
x
gap> poly:=x^8-2;
x^8-2
gap> g:=TransitiveGroup(Degree(poly),GaloisType(poly));
2D_8(8)=[D(4)]2
gap> IdGroup(g);
[ 16, 8 ]
gap> f1:=x^5-x-1;
x^5-x-1
gap> IdGroup(TransitiveGroup(Degree(f1),GaloisType(f1)));
[ 120, 34 ]
gap> IdGroup(SymmetricGroup(5));
[ 120, 34 ]
这是一个非可解扩张的伽罗瓦扩张:记K是f(x)=x^5-x-1∈Q[x]的分裂域,则Gal(K/Q)=S_5(一种不可解群),所以K/Q是非可解扩张的伽罗瓦扩张。又记作G(x^5-x-1,Q)=S_5。
gap> f2:=x^3-2;
x^3-2
gap> IdGroup(TransitiveGroup(Degree(f2),GaloisType(f2)));
[ 6, 1 ]
gap> e2:=AlgebraicExtension(Rationals,f2);
<algebraic extension over the Rationals of degree 3>
gap> IsAlgebraicExtension(e2);
true
gap> IsField(e2);
true
这是一个非阿贝尔扩张的可解扩张:记K是f(x)=x^3-2∈Q[x]的分裂域,则Gal(K/Q)=S_3(一种非幂零的超可解群),所以K/Q是非阿贝尔扩张的可解扩张。
gap> x:=Indeterminate(Rationals);
x
gap> f4:=x^3+2;
x^3+2
gap> IdGroup(TransitiveGroup(Degree(f4),GaloisType(f4)));
[ 6, 1 ]
这也是一个非阿贝尔扩张的可解扩张:x^3+2在Q上的分裂域是Q(e^(2pii/3),2^(1/3))=Q(r_1,r_2,r_3)。
gap> f3:=x^4-10*x^2+1;
x^4-10*x^2+1
gap> IdGroup(TransitiveGroup(Degree(f3),GaloisType(f3)));
[ 4, 2 ]
这是一个非循环扩张的阿贝尔扩张,例如多项式x^4-10x^2+1=(x^2-5)^2-24有四个根:x_1=sqrt(2)+sqrt(3),x_2=sqrt(2)-sqrt(3),x_3=-sqrt(2)+sqrt(3),x_4=-sqrt(2)-sqrt(3)。伽罗瓦群是Klein四元群(一种非循环的阿贝尔群),所以扩张Q(sqrt(2),sqrt(3))/Q是非循环扩张的阿贝尔扩张。(x^2-2)(x^2-3)在Q上的分裂域是Q(sqrt(2),sqrt(3))=Q(sqrt(2)+sqrt(3))。Q(sqrt(2))/Q是二次扩张,Q(sqrt(2),sqrt(3))/Q(sqrt(2))是二次扩张=>Q(sqrt(2),sqrt(3))/Q是四次扩张。
gap> IdGroup(GaloisGroup(Field(Sqrt(2))));
[ 2, 1 ]
gap> IdGroup(GaloisGroup(Field(Sqrt(-2))));
[ 2, 1 ]
这是二次循环扩张的例子:①Gal(Q(sqrt(2))/Q)=C_2,[Q(sqrt(2)):Q]=|C_2|=2。x^2-2和x^4-4在Q上的分裂域都是Q(sqrt(2)),其伽罗瓦群都是C_2。Q(sqrt(2))/Q是正规域扩张,它包括了x^2-2的所有根。②Gal(Q(sqrt(3))/Q)=C_2,[Q(sqrt(3)):Q]=|C_2|=2。x^2-4x+1在Q上的分裂域是Q=(2+sqrt(3),2-sqrt(3))=Q(sqrt(3)),其伽罗瓦群是C_2。按:Q的以下两个单代数扩域是同构的:Q(sqrt(2))=Q(sqrt(3)),其中同构映射f:a+bsqrt(2)->a+bsqrt(3)。一般地,若g(x)是某域F上的n次不可约多项式,a和b是g(x)的两个根,则F(a)和F(b)是同构的单代数扩域。
这是Gal(Q/Q)=C_1的例子: x^2-4x+4=(x-2)^2和x^2-3x+2=(x-2)(x-1)在Q上的分裂域为Q,其伽罗瓦群是平凡的。
考虑多项式f(x)=x^2+1∈Q[x]
f(x)在C中是分裂的,但它在Q上的分裂域是Q(i)={a+bi|a,b∈Q}
f(x)在R上的分裂域是C。
考虑多项式f(x)=x^2-3∈Q[x]
f(x)在R中是分裂的,但它在Q上的分裂域是Q(sqrt(3))={a+bsqrt(3)|a,b∈Q}(它也等于Q[sqrt(3)])。
gap> x := Indeterminate( Rationals, "x" );
x
gap> f := UnivariatePolynomial( Rationals, [1,0,1] );
x^2+1
gap> L := SplittingField( f );
<algebraic extension over the Rationals of degree 2>
gap> IdGroup(GaloisGroupOnRoots(f));
[ 2, 1 ]
gap> f1 := UnivariatePolynomial( Rationals, [-3,0,1] );
x^2-3
gap> L1 := SplittingField( f1 );
<algebraic extension over the Rationals of degree 2>
gap> IdGroup(GaloisGroupOnRoots(f1));
[ 2, 1 ]
假定F=F_2,α是F[x]中不可约多项式x^2+x+1的一个根,证明F(α)={0,1,α,1+α}是一个含4个元素的域。求多项式x^2+x+1的另一个根。
gap> x:=X(GF(2),"x");
x
gap> f:=x^2+x+1;
x^2+x+Z(2)^0
gap> IsIrreducible(f);
true
gap> F:=AlgebraicExtension(GF(2),f);
<algebra-with-one of dimension 2 over GF(2)>
gap> a:=RootOfDefiningPolynomial(F);
a
gap> a^2;a^3;a^4;
a+Z(2)^0
!Z(2)^0
a
gap> a+a;a+a+a;a+a+a+a;
!0*Z(2)
a
!0*Z(2)
gap> Elements(F);
[ !0*Z(2), a, !Z(2)^0, a+Z(2)^0 ]
gap> Factors(f);
[ x^2+x+Z(2)^0 ]
伽罗瓦域GF(p^m)给出了伽罗瓦群的一个特别简单的例子,这里是把它包含的素域GF(p)作为基域。Gal(GF(p^m)/GF(p))是m阶的循环群。
gap> IdGroup(GaloisGroup(GF(256)));
[ 8, 1 ]
gap> IdGroup(GaloisGroup(AsField(GF(2),GF(256))));
[ 8, 1 ]
gap> IdGroup(GaloisGroup(AsField(GF(4),GF(256))));
[ 4, 1 ]
gap> IdGroup(GaloisGroup(AsField(GF(4),GF(4096))));
[ 6, 2 ]
gap> IdGroup(GaloisGroup ( GF(32)));
[ 5, 1 ]
gap> IdGroup(GaloisGroup ( GF(16)));
[ 4, 1 ]
gap> IdGroup(GaloisGroup ( GF(8)));
[ 3, 1 ]
gap> IdGroup(GaloisGroup ( GF(4)));
[ 2, 1 ]
gap> IdGroup(GaloisGroup ( GF(2)));
[ 1, 1 ]
gap> IdGroup(GaloisGroup(GF(3)));
[ 1, 1 ]
gap> IdGroup(GaloisGroup ( GF(9)));
[ 2, 1 ]
gap> IdGroup(GaloisGroup ( GF(27)));
[ 3, 1 ]
gap> IdGroup(GaloisGroup ( GF(81)));
[ 4, 1 ]
记F=Z_2是含2个元素的域,证明多项式x^2+1在多项式环F[x]中可约,而x^2+x+1在多项式环F[x]中不可约。
gap> x:=Indeterminate(GF(2));
x_1
gap> f := UnivariatePolynomial(GF(2), [1,1,1] );
#I Convert coefficient list to get compatibility with family
x_1^2+x_1+Z(2)^0
gap> L := SplittingField( f );
GF(2^2)
gap> IdGroup(GaloisGroup(AsField(GF(2),L)));
[ 2, 1 ]
n次分圆域是多项式x^n-1的分裂域,因此是有理数域的伽罗瓦扩域。
这个扩张的次数等于欧拉φ函数:[Q(ζ_n):Q]=φ(n)
Gal(Q(ζ_n)/Q)=(Z_n)^×——这个群是偶数阶交换群
gap> Phi(60);
16
gap> IdGroup(GaloisGroup(CyclotomicField(60)));
[ 16, 10 ]
正五边形的作图可能性在古希腊就已经知道了。
取a=ζ_5。
Gal(Q(ζ_5)/Q)=(Z/5Z)^×=F_5^×=C_4。
设E为x^8-1在Q上的分裂域。问[E:Q]=?并确定伽罗瓦群Gal(E/Q)。
取a=ζ_17。
Gal(Q(ζ_17)/Q)=(Z/17Z)^×=F_17^×=C_16。
gap> IdGroup(GaloisGroup(CF(5)));
[ 4, 1 ]
gap> IdGroup(GaloisGroup(CF(8)));
[ 4, 2 ]
gap> IdGroup(GaloisGroup(CF(15)));
[ 8, 2 ]
gap> IdGroup(GaloisGroup(CF(17)));
[ 16, 1 ]
U(8) ={[1]_8,[3]_8,[5]_8,[7]_8}=K_4≠C_4,
U(15)=U(3)×U(5)=C_2×C_4,
定理:n>=3且n≠6时,n次对称群的自同构都是内自同构,且Aut(S_n)=S_n。无限循环群的自同构群是C_2,C_n的自同构群是一个φ(n)阶群。
由于无限循环群有两个生成元,C_n有φ(n)个生成元,从而其自同构群分别为C_2和φ(n)阶群。令G与H是两个阶为互素的有限群,则Aut(G×H)=Aut(G)×Aut(H)。
gap> IdGroup(AutomorphismGroup(DihedralGroup(12)));
[ 12, 4 ]
gap> IdGroup(AutomorphismGroup(SmallGroup(12,5)));
[ 12, 4 ]
gap> IdGroup(DihedralGroup(12));
[ 12, 4 ]
gap> IdGroup(DirectProduct(SmallGroup(4,2),CyclicGroup(3)));
[ 12, 5 ]
gap> IdGroup(AutomorphismGroup(CyclicGroup(3)));
[ 2, 1 ]
Aut(C_3×C_2×C_2)=Aut(C_3)×Aut(C_2×C_2)=S_3×C_2=D_3×C_2=D_6
gap> IdGroup(AutomorphismGroup(CyclicGroup(2)));
[ 1, 1 ]
gap> IdGroup(AutomorphismGroup(CyclicGroup(6)));
[ 2, 1 ]
gap> Phi(6);
2
gap> IdGroup(AutomorphismGroup(Group((1,2,3,4,5))));
[ 4, 1 ]
gap> IdGroup(AutomorphismGroup(CyclicGroup(5)));
[ 4, 1 ]
gap> IdGroup(AutomorphismGroup(SmallGroup(4,2)));
[ 6, 1 ]
K_4有3个2阶群元,3个元素共有3!=6个排列,从而K_4有6个自同构。所以Aut(K_4)=S_3。
gap> IdGroup(AutomorphismGroup(QuaternionGroup(8)));
[ 24, 12 ]
??Aut(Q_8)=S_3,i,j,k的阶都是4
gap> IdGroup(AutomorphismGroup(SymmetricGroup(6)));
[ 1440, 5841 ]
gap> IdGroup(AutomorphismGroup(SymmetricGroup(5)));
[ 120, 34 ]
gap> IdGroup(AutomorphismGroup(SymmetricGroup(4)));
[ 24, 12 ]
gap> IdGroup(AutomorphismGroup(SymmetricGroup(3)));
[ 6, 1 ]
Aut(S_3)=S_3
gap> IdGroup(AutomorphismGroup(SymmetricGroup(2)));
[ 1, 1 ]
gap> IdGroup(AutomorphismGroup(SymmetricGroup(1)));
[ 1, 1 ]
gap> IdGroup(AutomorphismGroup(DihedralGroup(8)));
[ 8, 3 ]
Aut(D_4)=D_4
N阶导出群的例子:
(S_3)^(1)=A_3,(S_3)^(2)={1}=>S_3是可解群
(S_4)^(1)=A_4,(S_3)^(2)=V_4,(S_3)^(3)={1}=>S_4是可解群
gap> DerivedSeriesOfGroup(SmallGroup(6,1));
[ <pc group of size 6 with 2 generators>, Group([ f2 ]), Group([ ]) ]
gap> DerivedLength(SmallGroup(6,1));
2
gap> List(DerivedSeriesOfGroup(SmallGroup(6,1)),IdGroup);
[ [ 6, 1 ], [ 3, 1 ], [ 1, 1 ] ]
gap> List(DerivedSeriesOfGroup(SmallGroup(6,1)),Size);
[ 6, 3, 1 ]
gap> List(DerivedSeriesOfGroup(SymmetricGroup(4)),IdGroup);
[ [ 24, 12 ], [ 12, 3 ], [ 4, 2 ], [ 1, 1 ] ]
http://world.std/~jmccarro/math/SmallGroups/SmallGroups.html
注意:这个网站中的有限群编号与GAP4 ID不一致
群24.4=GAP4(24,1)
gap> IdGroup(Group((1,13,7,19,4,16,10,22)(2,15,8,21,5,18,11,24)(3,14,9,20,6,17,12,23), (1,7,4,10)(2,8,5,11)(3,9,6,12)(13,19,16,22)(14,20,17,23)(15,21,18,24), (1,4)(2,5)(3,6)(7,10)(8,11)(9,12)(13,16)(14,17)(15,18)(19,22)(20,23)(21,24), (1,2,3)(4,5,6)(7,8,9)(10,11,12)(13,14,15)(16,17,18)(19,20,21)(22,23,24)));
[ 24, 1 ]
gap> IdGroup(Center(SmallGroup(24,1)));
[ 4, 1 ]
群24.5=GAP4(24,3)
gap> IdGroup(Group((1,2)(3,4)(5,6)(7,8),(1,8,2,7)(3,6,4,5),(1,6,2,5)(3,7,4,8),(3,7,5)(4,8,6)));
[ 24, 3 ]
gap> IdGroup(Center(SmallGroup(24,3)));
[ 2, 1 ]
群24.6=GAP4(24,4)
gap> IdGroup(Group((1,13,4,16)(2,15,5,18)(3,14,6,17)(7,22,10,19)(8,24,11,21)(9,23,12,20), (1,7,4,10)(2,8,5,11)(3,9,6,12)(13,19,16,22)(14,20,17,23)(15,21,18,24), (1,4)(2,5)(3,6)(7,10)(8,11)(9,12)(13,16)(14,17)(15,18)(19,22)(20,23)(21,24), (1,2,3)(4,5,6)(7,8,9)(10,11,12)(13,14,15)(16,17,18)(19,20,21)(22,23,24)));
[ 24, 4 ]
gap> IdGroup(Center(SmallGroup(24,4)));
[ 2, 1 ]
群24.7=GAP4(24,5)
gap> IdGroup(Group((1,3,2)(4,6,5)(7,9,8)(10,12,11), (1,4)(2,5)(3,6)(7,10)(8,11)(9,12), (1,7,4,10)(2,8,5,11)(3,9,6,12), (2,3)(5,6)(8,9)(11,12)));
[ 24, 5 ]
gap> IdGroup(Center(SmallGroup(24,5)));
[ 4, 1 ]
群24.11=GAP4(24,10)
gap> IdGroup(Group((1,2)(3,4)(5,6), (1,7)(2,8)(3,9)(4,10)(5,11)(6,12), (1,3,5)(2,4,6)(7,9,11)(8,10,12), (7,8)(9,10)(11,12)));
[ 24, 10 ]
gap> IdGroup(Center(SmallGroup(24,10)));
[ 6, 2 ]
群24.12=GAP4(24,11)
gap> IdGroup(Group((1,13,2,14)(3,15,4,16)(5,17,6,18)(7,20,8,19)(9,22,10,21)(11,24,12,23), (1,7,2,8)(3,9,4,10)(5,11,6,12)(13,19,14,20)(15,21,16,22)(17,23,18,24), (1,3,5)(2,4,6)(7,9,11)(8,10,12)(13,15,17)(14,16,18)(19,21,23)(20,22,24), (1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)));
[ 24, 11 ]
gap> IdGroup(Center(SmallGroup(24,11)));
[ 6, 2 ]
群24.13=GAP4(24,12)
gap> IdGroup(Group((1,4)(2,3), (1,3)(2,4), (2,3), (2,3,4)));
[ 24, 12 ]
gap> IdGroup(Center(SmallGroup(24,12)));
[ 1, 1 ]
称辛群对它中心的商群Sp_n(F)/C为射影辛群,用PSp_n(F)表示。
定理:射影辛群PSp_n(F)是单群,除r=1,|F|=2或3和r=2,|F|=2,其中2r=n。
有限域F_q上辛群PSp_(2r)(F_q)的阶为:(q^(2r)-1)q^(2r-1)(q^(2r-2)-1)q^(2r-3)…(q^2-1)q。
Sp_4(F_2)=S_6(720阶群)。
gap> IdGroup(Sp(4,2));
[ 720, 763 ]
gap> IdGroup(SymmetricGroup(6));
[ 720, 763 ]
gap> IdGroup(PSp(4,2));
[ 720, 763 ]
定理:SL_2(K){<|}GL_2(K)。
SL_2(F_3)是一个24阶群2T,它有一个8阶的正规子群
gap> IdGroup(SL(2,3));
[ 24, 3 ]
PSL(2,2)=GL_2(F_2)=SL_2(F_2)=S_3
gap> IdGroup(PSL(2,2));
[ 6, 1 ]
gap> IdGroup(GL(2,2));
[ 6, 1 ]
gap> IdGroup(SL(2,2));
[ 6, 1 ]
称因子群SL_n(F)/C(SL_n(F))为射影特殊线性群,用PSL_n(F)表示。
定理:设n>=2,则除非n=2及F=F_2或F_3,PSL_n(K)是单群。
PSL(2,3)=T=A_4
gap> IdGroup(AlternatingGroup(4));
[ 12, 3 ]
gap> IdGroup(PSL(2,3));
[ 12, 3 ]
gap> IdGroup(GO(0,3,2));
[ 6, 1 ]
gap> IdGroup(GO(0,3,3));
[ 48, 48 ]
gap> IdGroup(GO(0,3,5));
[ 240, 189 ]
gap> IdGroup(GO(0,3,7));
[ 672, 1254 ]
gap> IdGroup(GO(-1,2,2));
[ 6, 1 ]
gap> IdGroup(GO(-1,2,3));
[ 8, 3 ]
gap> IdGroup(GO(-1,2,5));
[ 12, 4 ]
gap> IdGroup(GO(-1,2,7));
[ 16, 7 ]
gap> IdGroup(GO(-1,4,2));
[ 120, 34 ]
gap> IdGroup(GO(-1,4,3));
[ 1440, 5842 ]
gap> IdGroup(SpecialOrthogonalGroup(1,2,2));
[ 2, 1 ]
gap> IdGroup(SO(1,2,2));
[ 2, 1 ]
gap> IdGroup(GO(1,2,2));
[ 2, 1 ]
gap> IdGroup(GO(1,2,3));
[ 4, 2 ]
gap> IdGroup(GO(1,2,5));
[ 8, 3 ]
gap> IdGroup(GO(1,2,7));
[ 12, 4 ]
gap> IdGroup(GO(1,4,2));
[ 72, 40 ]
gap> IdGroup(GO(1,4,3));
[ 1152, 157478 ]
gap> Order(GO(1,4,4));
7200
1阶环即零环{0}
gap> NumberSmallRings(1);
1
gap> R:=SmallRing(1,1);
<ring with 1 generators>
gap> Elements(R);
[ 0*a ]
gap> GeneratorsOfRing(R);
[ a ]
gap> ShowAdditionTable(R);
+ | 0*a
----+----
0*a | 0*a
gap> ShowMultiplicationTable(R);
* | 0*a
----+----
0*a | 0*a
2阶环有2个:
gap> NumberSmallRings(2);
2
SmallRing(2,2)=GF(2)和SmallRing(2,1)=M_2=M_2(M_2^+=C_2)(称为加群为C_2的2阶零乘环),它们都是C_2的强抽象。
3阶环有2个:
gap> NumberSmallRings(3);
2
SmallRing(3,2)=GF(3)和SmallRing(3,1)=M_3=M_3(M_3^+=C_3)(称为加群为C_3的3阶零乘环)。
注意:同一个Abel群可以强抽象出不同构的多个环。Z_6的子环R={[0],[2],[4]}=Z_3=GF(3)与Z_9的子环S={[0],[3],[6]}=M_3=M_3(M_3^+=C_3)都是3阶循环环,但它们不同构。[作为加群同构但作为环不同构的有限循环环的例子]
5阶环有2个:
gap> NumberSmallRings(5);
2
SmallRing(5,2)=GF(5)和SmallRing(5,1)=M_5=M_5(M_5^+=C_5)(称为加群为C_5的5阶零乘环)
6阶环有4个:
gap> NumberSmallRings(6);
4
ring 6.Nu.1=M_6(M_6^+=C_6)={[0],[6],[12],[18],[24],[30]}
gap> R:=SmallRing(6,1);
<ring with 1 generators>
gap> ShowMultiplicationTable(R);
* | 0*a a 2*a 3*a 4*a -a
----+------------------------
0*a | 0*a 0*a 0*a 0*a 0*a 0*a
a | 0*a 0*a 0*a 0*a 0*a 0*a
2*a | 0*a 0*a 0*a 0*a 0*a 0*a
3*a | 0*a 0*a 0*a 0*a 0*a 0*a
4*a | 0*a 0*a 0*a 0*a 0*a 0*a
-a | 0*a 0*a 0*a 0*a 0*a 0*a
ring 6.Nu.2=R_2(R_2^+=C_6)={[0],[2],[4],[6],[8],[10]}
gap> R:=SmallRing(6,2);
<ring with 1 generators>
gap> ShowMultiplicationTable(R);
* | 0*a a 2*a 3*a 4*a -a
----+------------------------
0*a | 0*a 0*a 0*a 0*a 0*a 0*a
a | 0*a 4*a 2*a 0*a 4*a 2*a
2*a | 0*a 2*a 4*a 0*a 2*a 4*a
3*a | 0*a 0*a 0*a 0*a 0*a 0*a
4*a | 0*a 4*a 2*a 0*a 4*a 2*a
-a | 0*a 2*a 4*a 0*a 2*a 4*a
ring 6.Nu.3=R_3(R_3^+=C_6)={[0],[3],[6],[9],[12],[15]}
gap> R:=SmallRing(6,3);
<ring with 1 generators>
gap> ShowMultiplicationTable(R);
* | 0*a a 2*a 3*a 4*a -a
----+------------------------
0*a | 0*a 0*a 0*a 0*a 0*a 0*a
a | 0*a 3*a 0*a 3*a 0*a 3*a
2*a | 0*a 0*a 0*a 0*a 0*a 0*a
3*a | 0*a 3*a 0*a 3*a 0*a 3*a
4*a | 0*a 0*a 0*a 0*a 0*a 0*a
-a | 0*a 3*a 0*a 3*a 0*a 3*a
ring 6.u.1=Z_6={[0],[1],[2],[3],[4],[5]}
Z_2={[0],[1]}与Z_3={[0],[1],[2]}的外直和为Z_6,Z_6是其子环(也是理想)Z_2={[0],[3]}与Z_3={[0],[2],[4]}的内直和。在同构意义下,外直和与内直和二者是一致的。
gap> R:=SmallRing(6,4);
<ring with 1 generators>
gap> ShowMultiplicationTable(R);
* | 0*a a 2*a 3*a 4*a -a
----+------------------------
0*a | 0*a 0*a 0*a 0*a 0*a 0*a
a | 0*a a 2*a 3*a 4*a -a
2*a | 0*a 2*a 4*a 0*a 2*a 4*a
3*a | 0*a 3*a 0*a 3*a 0*a 3*a
4*a | 0*a 4*a 2*a 0*a 4*a 2*a
-a | 0*a -a 4*a 3*a 2*a a
定理:在所有的n阶循环环中,有而且只有T(n)(n的正因数个数)个是互不同构的。
C_n有而且只有T(n)个子群=>n阶循环环有而且只有T(n)个子环。
环Z_6=SmallRing(6,4)有T(6)=4个子环:{[0]},{[0],[3]},{[0],[2],[4]},Z_6
gap> S:=Subrings(SmallRing(6,4));
[ <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators> ]
gap> Size(S);
4
gap> List(S,GeneratorsOfRing);
[ [ 0*a ], [ 3*a ], [ 2*a ], [ a ] ]
gap> Elements(S[1]);
[ 0*a ]
gap> ShowMultiplicationTable(S[1]);
* | 0*a
----+----
0*a | 0*a
gap> ShowMultiplicationTable(S[2]);
* | 0*a 3*a
----+--------
0*a | 0*a 0*a
3*a | 0*a 3*a
gap> ShowMultiplicationTable(S[3]);
* | 0*a 2*a 4*a
----+------------
0*a | 0*a 0*a 0*a
2*a | 0*a 4*a 2*a
4*a | 0*a 2*a 4*a
gap> ShowMultiplicationTable(S[4]);
* | 0*a a 2*a 3*a 4*a -a
----+------------------------
0*a | 0*a 0*a 0*a 0*a 0*a 0*a
a | 0*a a 2*a 3*a 4*a -a
2*a | 0*a 2*a 4*a 0*a 2*a 4*a
3*a | 0*a 3*a 0*a 3*a 0*a 3*a
4*a | 0*a 4*a 2*a 0*a 4*a 2*a
-a | 0*a -a 4*a 3*a 2*a a
Z/6Z的全部理想有4个:Z_1,F_2,F_3,Z/6Z。
gap> I:=Ideals(SmallRing(6,4));
[ <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators> ]
gap> R:=SmallRing(6,4);I:=Ideals(R);
<ring with 1 generators>
[ <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators> ]
gap> Q:=R/I[4];
<ring with 1 generators>
gap> ShowMultiplicationTable(Q);
* | 0*a
----+----
0*a | 0*a
gap> hom:= NaturalHomomorphismByIdeal(R,I[4]);
[ a ] -> [ 0*a ]
gap> Size(ImagesSource(hom));
1
gap> Size(R/I[3]);
3
gap> Size(R/I[2]);
2
gap> Size(R/I[1]);
6
gap> ShowMultiplicationTable(R/I[3]);
* | 0*q1 q1 -q1
-----+---------------
0*q1 | 0*q1 0*q1 0*q1
q1 | 0*q1 q1 -q1
-q1 | 0*q1 -q1 q1
1772年,欧拉发现了第8个梅森素数M8(10位数)。
gap> IsIrreducibleRingElement( Integers,2147483647);
true
gap> IsIrreducibleRingElement( Integers,2^31-1);
true
gap> IsPrime(Integers,2147483647);
true
gap> IsPrime(2147483647);
true
gap> IsPrime(GaussianIntegers,2147483647);
true
gap> IsPrime(GaussianIntegers,5);
false
gap> IsPrime(Integers,5);
true
gap> IsPrime(5);
true
gap> Factors(GaussianIntegers,5);
[ 2-E(4), 2+E(4) ]
gap> Factors(Integers,5);
[ 5 ]
gap> Factors(5);
[ 5 ]
gap> R:=PolynomialRing(Rationals,1);
Rationals[x_1]
gap> IsUniqueFactorizationRing(R);
true
gap> Units(GaussianIntegers);
[ -1, 1, -E(4), E(4) ]
gap> Units(Integers);
[ -1, 1 ]
gap> Units(ZmodnZ(4));
<group of size 2 with 1 generators>
gap> IdGroup(Units(ZmodnZ(4)));
[ 2, 1 ]
gap> IdGroup(Units(ZmodnZ(60)));
[ 16, 10 ]
gap> q:= QuaternionAlgebra( Rationals );
<algebra-with-one of dimension 4 over Rationals>
gap> IsField( q ); IsDivisionRing( q );
false
true
gap> IsDivisionRing(GaussianRationals);
true
gap> Algebra( Rationals, [Sqrt(-1)] );
<algebra over Rationals, with 1 generators>
gap> GaussianRationals=Algebra( Rationals, [Sqrt(-1)] );
true
gap> GaussianRationals=Algebra( Rationals, [Sqrt(-3)] );
false
gap> Algebra( Rationals, [Sqrt(-3)] );
<algebra over Rationals, with 1 generators>
gap> IsField(GF(2));
true
gap> IsUniqueFactorizationRing(GF(2));
false
gap> IsIntegralRing(GF(2));
true
gap> IsDivisionRing(GF(2));
true
gap> IsField(Ring(Sqrt(2)));
false
gap> IsRing(Ring(Sqrt(2)));
true
gap> IsRing(GF(2));
true
gap> IsRing(CF(1));
true
gap> IsRing(CF(3));
true
gap> Ring(1);
Integers
gap> IsRing(Integers);
true
gap> IsRing(Ring(1));
true
gap> IsField(Ring(1));
false
gap> IsIntegralRing(Integers);
true
gap> IsUniqueFactorizationRing(Ring(1));
true
gap> IsUniqueFactorizationRing(Integers);
true
gap> IsEuclideanRing(Integers);
true
gap> IsField(Ring(-1));
false
gap> IsRing(Ring(-1));
true
gap> Ring(-1);
<ring with 1 generators>
gap> IsUniqueFactorizationRing(Ring(-1));
false
gap> IsUniqueFactorizationRing(GaussianIntegers);
true
gap> IsUniqueFactorizationRing(DefaultRing(E(4)));
true
gap> IsUniqueFactorizationRing(Ring(E(4)));
false
gap> IsRing(Ring(E(4)));
true
gap> IsField(Ring(E(4)));
false
gap> DefaultRing(2,E(4));
GaussianIntegers
gap> DefaultRing(E(4));
GaussianIntegers
gap> IsRing(ZmodnZ(4));
true
gap> IsField(ZmodnZ(4));
false
gap> IsRing(ZmodnZ(5));
true
gap> IsField(ZmodnZ(5));
true
gap> IsField(Ring(CF(8)));
false
gap> IsRing(CF(8));
true
gap> IsRing(Ring(CF(8)));
true
gap> IsIntegralRing(CF(8));
true
两类不同的素域,从同构的意义上说任何域都可以看成有理数域Q的扩域或者p元域Fp的扩域
?p进域呢
定理:素域F只有以下两种:
(1)char F=0时F≌Q(有理数域),
(2)char F=p时F≌Fp。
R的特征为0,记为char R=0。
R的特征为p,记为char R=p。
素域与扩域的定义:设K是一个域,如果K的非空子集F在K的加法与乘法运算之下也成为一个域,则F称为K的子域,而K称为F的扩域。
一个域如果不包含更小的子域,则称为素域。因为若干个子域的交集还是一个子域,因此素域是存在的而且也是唯一的。
gap> IsPrimeField(GF(2));
true
gap> IsPrimeField(GaussianRationals);
false
gap> IsPrimeField(CF(4));
false
gap> CF(4);
GaussianRationals
gap> IsPrimeField(GF(3));
true
gap> IsPrimeField(GF(9));
false
gap> IsPrimeField(Rationals);
true
gap> IsPrimeField(CF(1));
true
gap> IsPrimeField(CF(2));
true
gap> CF(1);
Rationals
gap> CF(1)=CF(2);
true
有理数域是素域
gap> IsRing(Rationals);
true
gap> IsIntegralRing(Rationals);
true
gap> IsUniqueFactorizationRing(Rationals);
false
gap> IsField(Rationals);
true
Q是无限整环,是无限域
gap> IsPrimeField(Field(Sqrt(2)));
false
gap> IsPrimeField(Field(Sqrt(-2)));
false
gap> IsPrimeField(CF(3));
false
gap> KG := GroupRing( GF(3), DihedralGroup(16) );
<algebra-with-one over GF(3), with 4 generators>
gap> L := LieAlgebra ( KG );
#I LAGUNA package: Constructing Lie algebra ...
<Lie algebra over GF(3)>
gap> IsLieAlgebraByAssociativeAlgebra( L );
true
20151026添加:
gap> LoadPackage("guava");
true
gap> q:=5;F:=GF(q);R:=PolynomialRing(F,2);;
5
GF(5)
gap> vars:=IndeterminatesOfPolynomialRing(R);x:=vars[1];y:=vars[2];
[ x_1, x_2 ]
x_1
x_2
gap> crv:=AffineCurve(y^3-x^3-x-1,R);
rec( polynomial := -x_1^3+x_2^3-x_1-Z(5)^0, ring := GF(5)[x_1,x_2] )
gap> g:=GenusCurve(crv);
1
gap> crv:=AffineCurve(y^2-x^3,R);
rec( polynomial := -x_1^3+x_2^2, ring := GF(5)[x_1,x_2] )
gap> g:=GenusCurve(crv);
1
定义在域F上的仿射代数曲线可以看作是F_n中由若干个n-元多项式定义的公共零点,使得其维数为一。
1.亏格为0的曲线:这种曲线至少有一个有理点在上面,在仿射或射影空间中,有理点是明显的或容易找到的。
2.亏格为1的曲线:这种曲线至少有一个可见的有理点和一个可见的有理对。
定理:设两三次曲线交9个点,如果第三条三次曲线过其中8个点,那么它一定过第九个点。
定理(2000):设两曲线Cm和Cn交mn个点,如果第三条曲线Cm+n-k过其中mn-(k-2)个点,那么它一定过剩下的k-2个点。
三次曲线的分类早在Newton那里就已经开始了,最后划分为72类。牛顿1707年证明在坐标变换下三次曲线有标准方程:y^2=x^3+ax^2+bx+c
椭圆曲线可以由Weierstrass的P-函数参数化:x=P(u), y=P´(u)
椭圆曲线上的群结构(点之间可定义加法):P+0=P;P+V=0;P+Q=Q+P;(P+Q)+R=P+(Q+R).
高观点下的初等数学3.(德国)克莱因
chap27从精确理论观点讨论平面几何
若一条曲线可以通过直尺机械产生,它就是代数曲线。
比代数曲线更为特殊的是有理曲线。
一般,我们把能嵌入到复射影空间的光滑复流形都称为代数流形。
L(D)-L(K-D)=degD-g+1
dim ker@-dim coker@=1-g
弄明白什么叫“除子”,才可以真正明白Riemann-Roch定理。Riemann-Roch定理的前身是Riemann不等式:dimF>=1+n-g,dimF是紧Riemann曲面M上的亚纯函数(由极点控制)集合F构成的向量空间的维数,g是M的亏格。1864年,Riemann的学生Roch在不等式的左边添加一项而使之成为如今的Riemann-Roch定理:dimF-dimD=1+n-g,dimD表示在每个极点处有不小于一阶零点的全纯微 分构成的向量空间的维数。 20151119添加:
Gauss超几何函数
For scalar a, b, and c, hypergeom([a,b],c,z) is the Gauss hypergeometric function 2F1(a,b;c;z).
>> doc hypergeom
>> y=hypergeom(1,1,1) y = 2.7183 >> y=hypergeom([1,1],1,1) y = NaN + Infi
chap4重要的组合数
4.1二项式系数
对于正整数n及非负整数k,n>=k,称二项式定理中的系数(n,k)=[n]_k/k!为二项式系数。
? binomial(5,2)
%3 = 10
4.3高斯二项式系数
对指定常数q及非负整数n,r,定义高斯二项式系数为
命题:Gauss二项式系数的组合意义是:q为素数幂时[n,r]是GF(q)上n维向量空间的r维子空间个数。
命题:[n,r]_q是q的r(n-r)次多项式,且lim[q->1][n,r]_q=(n,r)。此时称[n,r]_q是(n,r)的q模拟。
gap> LoadPackage("quagroup");
|
| QuaGroup
|
----------- A package for dealing with quantized enveloping algebras
|
| Willem de Graaf
| degraaf@science.unitn.it true
gap> GaussianBinomial( 5, 2, _q^2 );
q^12+q^8+2*q^4+2+2*q^-4+q^-8+q^-12
gap> GaussianBinomial( 5, 2, _q);
q^6+q^4+2*q^2+2+2*q^-2+q^-4+q^-6
gap> GaussianBinomial( 5, 0, _q);
1
gap> GaussianBinomial( 5, 6, _q);
0
gap> GaussianBinomial( 5, 3, _q);
q^6+q^4+2*q^2+2+2*q^-2+q^-4+q^-6
chap9波利亚计数理论
1937年,(匈牙利-美)波利亚(G.Polya,1887-1985)提出波利亚计数定理。
9.1作用在集合上的群
对群G的两个子群H1和H2,若存在g∈G使得gH1g^-1=H2,则称这两个子群是彼此共轭的。
对于x∈X,称X的子集θ(x)为x所在的轨(orbit)。X中的两元同轨关系是一种等价关系。轨θ(x)即是X在G作用下所划分成的等价类(或称传递集、可迁集、可迁类)。对于x∈X,称G_x为x的稳定核(stabilizer)。
称|G|为G的阶,|X|为G的度。
命题9.1.1:稳定核是G的子群,而同一轨中各元的稳定核是彼此共轭的。
命题9.1.2:对于x∈X,有|G|=|θ(x)|•|G_x|。
六面体群(阶为24)分别作用于立方体的顶点集(度为8)、棱集合(度为12)与面集合(度为6)时
X90表示绕X轴顺时针旋转90°,对应P1X90=P2;
y90表示绕Y轴逆时针旋转90°,对应y90P1=P2。
http://www.doc88/p-692153995466.html
gap> X90:=[[1,0,0],[0,0,1],[0,-1,0]];;y90:=[[0,0,-1],[0,1,0],[1,0,0]];;C4:=GroupWithGenerators([X90]);;IdGroup(C4);G:=GroupWithGenerators([X90,y90]);;IdGroup(G);
[ 4, 1 ]
[ 24, 12 ]
gap> G:=SymmetricGroup(4);;IdGroup(G);cl:=ConjugacyClasses(G);
[ 24, 12 ]
[ ()^G, (1,2)^G, (1,2)(3,4)^G, (1,2,3)^G, (1,2,3,4)^G ]
gap> len:=Size(cl);for i in [1..len] do Print(Size(cl[i]),","); od;Print("\n");for i in [1..len] do Print(IdGroup(Centralizer(cl[i])),","); od;
5
1,6,3,8,6,
[ 24, 12 ],[ 4, 2 ],[ 8, 3 ],[ 3, 1 ],[ 4, 1 ],
gap> for i in [1..len] do Print(Representative(cl[i]),",",Size(cl[i]),",",Size(Centralizer(cl[i])),",",Elements(Centralizer(cl[i])),"\n");od;
(),1,24,[ (), (3,4), (2,3), (2,3,4), (2,4,3), (2,4), (1,2), (1,2)(3,4), (1,2,3), (1,2,3,4), (1,2,4,3), (1,2,4),
(1,3,2), (1,3,4,2), (1,3), (1,3,4), (1,3)(2,4), (1,3,2,4), (1,4,3,2), (1,4,2), (1,4,3), (1,4), (1,4,2,3),
(1,4)(2,3) ]
(1,2),6,4,[ (), (3,4), (1,2), (1,2)(3,4) ]
(1,2)(3,4),3,8,[ (), (3,4), (1,2), (1,2)(3,4), (1,3)(2,4), (1,3,2,4), (1,4,2,3), (1,4)(2,3) ]
(1,2,3),8,3,[ (), (1,2,3), (1,3,2) ]
(1,2,3,4),6,4,[ (), (1,2,3,4), (1,3)(2,4), (1,4,3,2) ]
9.2有关的群的运算
9.3置换群的轮换指标
9.4伯恩赛德引理
作用在X上的置换群G称为可迁的(transitive),若G在X上作用的轨道仅一个。对于正整数k,作用在X上的置换群G称为k可迁 的,若对X上的任两个k排列,存在某g∈G,可使其一个变为另一个。k>=2时的可迁亦可统称为重可迁。对¥t<=k,若G是k可迁的,则G亦是t可迁的。故一般所称的k可迁,常指最大可迁值。若G是k可迁的,而单位元是G中唯一固定k个点的置换,则G称为恰k可迁的。恰1可迁群称为在X上正则。
命题9.4.3:当n>=3时,对称群S_n是n可迁的,而交代群A_n是(n-2)可迁的。
9.5波利亚计数定理
9.6圈形排列问题
9.7图的计数多项式
9.8波利亚定理的推广
9.9波利亚定理的应用 gap> for q in [2..6] do l5:=q^6*(q^6-1)*(q^2-1);L5:=SmallSimpleGroup(l5);Print(l5,",",L5,"\n");od;
12096,fail
4245696,G(2, 3)
251596800,G(2, 4)
5859000000,G2(5)
76185748800,fail
gap> for q in [2..2] do l6:=q^24*(q^12-1)*(q^8-1)*(q^6-1)*(q^2-1);L6:=SmallSimpleGroup(l6);Print(l6,",",L6,"\n");od;
3311126603366400,F4(2)
gap> LoadPackage("sonata");
#I You may wish to install the xgap package
#I and enjoy the graphic capabilities of SONATA. ___________________________________________________________________________
/ ___
|| / \ /\ Version 2.6
|| || || |\ | / \ /\ Erhard Aichinger
\___ || || |\\ | /____\_____________/__\ Franz Binder
\ || || | \\ | / \ || / \ Juergen Ecker
|| \___/ | \\ | / \ || / \ Peter Mayr
|| | \\| / \ || Christof Noebauer
\___/ | \| || System Of Nearrings And Their Applications
Info: http://www.algebra.uni-linz.ac.at/Sonata/ true
gap> A4:=AlternatingGroup(4);;IdGroup(A4);InnA4:=InnerAutomorphisms(A4);;IdGroup(Group(InnA4));
[ 12, 3 ]
[ 12, 3 ]
1955年,谢瓦莱找出了一类单群——被称为谢瓦莱群;
http://brauer.maths.qmul.ac.uk/Atlas/v3/exc/G24/
gap> g:=SmallSimpleGroup(6048);Order(g);IsSimpleGroup(g);Order(SU(3,3));Order(GU(3,3));
PSU(3,3)
6048
true
6048
24192
gap> g:=SmallSimpleGroup(4245696);Order(g);IsSimpleGroup(g);
G(2, 3)
4245696
true
gap> g:=SmallSimpleGroup(251596800);Order(g);IsSimpleGroup(g);
G(2, 4)
251596800
true
gap> g:=SmallSimpleGroup(5859000000);Order(g);IsSimpleGroup(g);
G2(5)
5859000000
true
gap> g:=SmallSimpleGroup(3311126603366400);Order(g);IsSimpleGroup(g);
F4(2)
3311126603366400
true
gap> LoadPackage("unipot");
/======================================================\
! !
! GAP Package UNIPOT 1.2 !
! (Computations with elements of unipotent !
! subgroups of Chevalley Groups) !
! !
! by Sergei Haller <Sergei.Haller@math.uni-giessen.de> !
! !
! see ??unipot !
\======================================================/
true
E_7(3)的幺幂子群是3^63阶群
gap> g:= UnipotChevSubGr("E",7,GF(3));Order(g);
<Unipotent subgroup of a Chevalley group of type E7 over GF(3)>
1144561273430837494885949696427
gap> G:=CyclicGroup(3^63);
<pc group of size 1144561273430837494885949696427 with 63 generators>
E_6(2)的幺幂子群是2^36阶群
gap> g:= UnipotChevSubGr("E",6,GF(2));Order(g);
<Unipotent subgroup of a Chevalley group of type E6 over GF(2)>
68719476736
gap> G:=CyclicGroup(214841575522005575270400);
<pc group of size 214841575522005575270400 with 51 generators>
gap> L:= SimpleLieAlgebra( "E", 6, GF(2) );
<Lie algebra of dimension 78 over GF(2)>
gap> Size(L);
302231454903657293676544
E_8(7)的幺幂子群是7^120阶群
gap> g:= UnipotChevSubGr("E",8,GF(7));Order(g);
<Unipotent subgroup of a Chevalley group of type E8 over GF(7)>
258086210989349276047917817413172383631691140276099547911280598425927853437317437263620645695945672001
20151012添加: 矩阵A的特征多项式为|xE-A|
gap> A:=[ [ 1, 0,0], [ 1,0, 1 ], [ 0,1, 0] ];y:=CharacteristicPolynomial(A);Factors(y);A1:=TransposedMat(A);y1:=CharacteristicPolynomial(A1);Factors(y1);
[ [ 1, 0, 0 ], [ 1, 0, 1 ], [ 0, 1, 0 ] ]
x_1^3-x_1^2-x_1+1
[ x_1-1, x_1-1, x_1+1 ]
[ [ 1, 1, 0 ], [ 0, 0, 1 ], [ 0, 1, 0 ] ]
x_1^3-x_1^2-x_1+1
[ x_1-1, x_1-1, x_1+1 ]
gap> A100:=A^100;
[ [ 1, 0, 0 ], [ 50, 1, 0 ], [ 50, 0, 1 ] ]
向量内积
gap> theta:=[2,0,-1];;t:=ScalarProduct(theta,theta);
5
gap> theta1:=[2,0,0,0,-1,-1];;t1:=ScalarProduct(theta1,theta1);
6
gap> theta1:=[2,0,0,0,-1,-1];;theta2:=[1,-1,-1,-1,1,1];;theta3:=[1,1,1,1,1,1];;t12:=ScalarProduct(theta1,theta2);t13:=ScalarProduct(theta1,theta3);t23:=ScalarProduct(theta2,theta3);
0
0
0
gap> theta:=[1,E(3),E(3)^2];;t:=ScalarProduct(theta,theta);
0
//线性卷积conv
//1.000000 6.000000 16.000000 26.000000 31.000000 20.000000
gap> a:=[1,2,3,4];;b:=[1,4,5];;ProductCoeffs(a,b);
[ 1, 6, 16, 26, 31, 20 ]
gap> lo:= LieObject( [ [ 1, 0 ], [ 0, 1 ] ] );m:=UnderlyingRingElement(lo);lo*lo;m*m;
LieObject( [ [ 1, 0 ], [ 0, 1 ] ] )
[ [ 1, 0 ], [ 0, 1 ] ]
LieObject( [ [ 0, 0 ], [ 0, 0 ] ] )
[ [ 1, 0 ], [ 0, 1 ] ]
三维叉积对加法的分配律,线性性和雅可比恒等式表明:具有向量加法和叉积的R^3构成了一个Lie代数。
a × (b × c) + b × (c × a) + c × (a × b) = 0
雅可比恒等式就是下列等式:[X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0
Lie代数是满足雅可比恒等式的代数结构的一个主要例子。
注意,满足雅可比恒等式的代数结构不一定满足反交换律。
x^3/6+x^2/2+x+1无有理根
2x^3-5x^2+5x-3的有理根为3/2
x^3-6x^2+15x-14的有理根为2
x^3/6+x^2/2+x+1无重根
x^3-3*x-2有重根
gap> x:=Indeterminate(Rationals);RootsOfUPol(x^3/6+x^2/2+x+1);
x_1
[ ]
gap> x:=Indeterminate(Rationals);RootsOfUPol(2*x^3-5*x^2+5*x-3);
x_1
[ 3/2 ]
gap> x:=Indeterminate(Rationals);RootsOfUPol(x^3-6*x^2+15*x-14);
x_1
[ 2 ]
gap> x:=Indeterminate(Rationals,"x");;y:=x^3/6+x^2/2+x+1;y1:=Derivative(y);Gcd(y,y1);GcdOp(y,y1);RootsOfUPol(y);
1/6*x^3+1/2*x^2+x+1
1/2*x^2+x+1
1
1
[ ]
gap> x:=Indeterminate(Rationals,"x");;y:=x^3-3*x-2;y1:=Derivative(y);Gcd(y,y1);GcdOp(y,y1);RootsOfUPol(y);
x^3-3*x-2
3*x^2-3
x+1
x+1
[ 2, -1, -1 ]
有理数域上的一元多项式环模不可约多项式生成的理想得到的无限域
gap> R:=PolynomialRing(Rationals,1);x:=Indeterminate(Rationals);poly:=x^2+x+1;IsIrreducibleRingElement(R,poly);Degree(poly);Factors(poly);F:=FieldByPolynomial(poly);Size(F);IsField(F);IsPrimeField(F);IsFinite(F);IsRationalsPolynomialRing(F);
Rationals[x_1]
x
x^2+x+1
true
2
[ x^2+x+1 ]
<algebraic extension over the Rationals of degree 2>
infinity
true
false
false
false
问题:GAP求基域为有理数域的可约多项式(例如f(x)=x^4-5*x^2+6=0)的伽罗瓦群?
注意:GAP软件中多项式环的功能尚不完善
R:=PolynomialRing(Rationals,1);IsUniqueFactorizationRing(R);IsIntegralRing(R);IsEuclideanRing(R);IsIrreducibleRingElement(R,x^2-2);IsIrreducibleRingElement(R,x^4-10*x^2+1);IsIrreducibleRingElement(R,50-45*x-6*x^2+x^3);IsIrreducibleRingElement(R,x^4-5*x^2+6);
R:=PolynomialRing(Rationals,2);IsUniqueFactorizationRing(R);IsEuclideanRing(R);
R:=PolynomialRing(Integers,1);IsUniqueFactorizationRing(R);IsEuclideanRing(R);
R:=PolynomialRing(Integers,2);IsUniqueFactorizationRing(R);IsEuclideanRing(R);
R:=PolynomialRing(GaussianIntegers,1);IsUniqueFactorizationRing(R);
R:=PolynomialRing(GaussianIntegers,2);IsUniqueFactorizationRing(R);
R:=PolynomialRing(GaussianRationals,1);IsUniqueFactorizationRing(R);IsIntegralRing(R);IsEuclideanRing(R);IsIrreducibleRingElement(R,x^2-2);
R:=PolynomialRing(GaussianRationals,2);IsUniqueFactorizationRing(R);IsEuclideanRing(R);
R:=UnivariatePolynomialRing(Rationals,"x");IsUniqueFactorizationRing(R);IsIntegralRing(R);IsIrreducibleRingElement(R,x^2-2);
R:=UnivariatePolynomialRing(Integers,"x");IsUniqueFactorizationRing(R);
R:=UnivariatePolynomialRing(GaussianRationals,"x");IsUniqueFactorizationRing(R);IsIntegralRing(R);IsIrreducibleRingElement(R,x^2-2);
R:=UnivariatePolynomialRing(GaussianIntegers,"x");IsUniqueFactorizationRing(R);
求方程x^3-2x-5=0的根。
gap> x:=Indeterminate(Rationals);RootsOfUPol(x^3-2*x-5);
x_1
[ ]
求方程x^3+2x^2+10x-20的根。
gap> x:=Indeterminate(Rationals);RootsOfUPol(x^3+2*x^2+10*x-20);
x_1
[ ]
gap> x:=Indeterminate(Rationals);RootsOfUPol(50-45*x-6*x^2+x^3);
x_1
[ 10, 1, -5 ]
gap> poly:=x^3-2*x-5;IsIrreducibleRingElement(PolynomialRing(Rationals,1),poly);IsSeparablePolynomial(poly);Degree(poly);
x^3-2*x-5
true
true
3
gap> poly:=x^3+2*x^2+10*x-20;IsIrreducibleRingElement(PolynomialRing(Rationals,1),poly);IsSeparablePolynomial(poly);Degree(poly);
x^3+2*x^2+10*x-20
true
true
3
gap> poly:=50-45*x-6*x^2+x^3;IsIrreducibleRingElement(PolynomialRing(Rationals,1),poly);IsSeparablePolynomial(poly);Degree(poly);
x^3-6*x^2-45*x+50
false
true
3
gap> poly:=x^4-5*x^2+6;IsIrreducibleRingElement(PolynomialRing(Rationals,1),poly);IsSeparablePolynomial(poly);Degree(poly);Factors(poly);
x^4-5*x^2+6
false
true
4
[ x^2-3, x^2-2 ]
定义:设F为域,称F[x]中多项式f(x)是F上的可分多项式,如果它在F[x]中的任一不可约因子都无重根(允许f(x)有重根)。否则,称f(x)是F上的不可分多项式。
任一无重根的不可约多项式必是可分多项式,不可分多项式的任一倍式必是不可分多项式。
完全域F上的多项式必是可分多项式。因为特征数为0的域和有限域必是完全域,因此,只有在特征数为p的无限域上才可能存在不可分多项式和不可分元。
gap> poly:=x^2+x+1;IsIrreducibleRingElement(PolynomialRing(GF(2),1),poly);Degree(poly);Factors(poly);
x^2+x+Z(2)^0
true
2
[ x^2+x+Z(2)^0 ]
gap> f:= MinimalPolynomial( Rationals, Sqrt(2) );
x^2-2
sqrt(2)在Q上的最小多项式为x^2-2。
gap> f:= MinimalPolynomial( Rationals, Sqrt(-1) );
x^2+1
gap> f:= MinimalPolynomial( Rationals, Sqrt(2)+Sqrt(3) );
x^4-10*x^2+1
sqrt(2)+sqrt(3)在Q上的最小多项式为f(x)=x^4-10x^2+1
http://www.gap-system/Manuals/pkg/MatricesForHomalg/doc/chap3.html
gap> LoadPackage("RingsForHomalg");
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading AutoDoc 2014.08.21 (Generate documentation from GAP source code)
by Sebastian Gutsche ( http://wwwb.math.rwth-aachen.de/~gutsche/) and
Max Horn ( http://www.quendi.de/math).
Homepage: http://wwwb.math.rwth-aachen.de/~gutsche/gap_packages/AutoDoc
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading ToolsForHomalg 2014.12.08 (Provides special methods and knowledge propagation tools)
by Mohamed Barakat ( http://www.mathematik.uni-kl.de/~barakat/),
Sebastian Gutsche ( http://wwwb.math.rwth-aachen.de/~gutsche/), and
Markus Lange-Hegermann ( http://wwwb.math.rwth-aachen.de/~markus/).
Homepage: http://wwwb.math.rwth-aachen.de/~gutsche/gap_packages/ToolsForHomalg
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading MatricesForHomalg 2015.02.03 (Lazy evaluated matrices with clever operations for the homalg project)
by Mohamed Barakat ( http://www.mathematik.uni-kl.de/~barakat/),
Markus Lange-Hegermann ( http://wwwb.math.rwth-aachen.de/~markus/),
Martin Leuner ( http://wwwb.math.rwth-aachen.de/Mitarbeiter/leuner.php), and
Vinay Wagh ( http://www.iitg.ernet.in/vinay.wagh/).
Homepage: http://homalg.math.rwth-aachen.de/index.php/core-packages/matricesforhomalg
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading HomalgToCAS 2015.02.03 (A window to the outer world)
by Thomas Bächler ( http://wwwb.math.rwth-aachen.de/~thomas/),
Mohamed Barakat ( http://www.mathematik.uni-kl.de/~barakat/),
Simon Görtzen ( http://wwwb.math.rwth-aachen.de/~simon/),
Sebastian Gutsche ( http://wwwb.math.rwth-aachen.de/~gutsche/), and
Vinay Wagh ( http://www.iitg.ernet.in/vinay.wagh/).
Homepage: http://homalg.math.rwth-aachen.de/index.php/core-packages/homalgtocas
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading RingsForHomalg 2015.02.10 (Dictionaries of external rings for the homalg project)
by Mohamed Barakat ( http://www.mathematik.uni-kl.de/~barakat/),
Simon Goertzen ( http://wwwb.math.rwth-aachen.de/goertzen/),
Markus Kirschmer ( http://www.math.rwth-aachen.de/~Markus.Kirschmer/),
Markus Lange-Hegermann ( http://wwwb.math.rwth-aachen.de/~markus/),
Oleksandr Motsak ( http://www.mathematik.uni-kl.de/~motsak/),
Daniel Robertz ( http://wwwb.math.rwth-aachen.de/~daniel/),
Hans Schönemann ( http://www.mathematik.uni-kl.de/~hannes/),
Andreas Steenpaß (), and
Vinay Wagh ( http://www.iitg.ernet.in/vinay.wagh/).
Homepage: http://homalg.math.rwth-aachen.de/index.php/core-packages/ringsforhomalg
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
true
gap> ZZ:=HomalgRingOfIntegers();
Z
gap> IsHomalgRing(ZZ);
true
gap> IsHomalgRing(Integers);
false
gap> IsPreHomalgRing(ZZ);
false
gap> IsPreHomalgRing(Integers);
false
gap> Display( ZZ );
<An internal ring>
gap> Z256 := ZZ / 2^8;
Z/( 256 )
gap> Display( Z256 );
<A residue class ring>
gap> Z2 := Z256 / 6;
Z/( 256, 6 )
gap> BasisOfRows( MatrixOfRelations( Z2 ) );
<An unevaluated non-zero 1 x 1 matrix over an internal ring>
gap> Z2;
Z/( 2 )
gap> Display( Z2 );
<A residue class ring>
gap> F2 := HomalgRingOfIntegers()/2;
Z/( 2 )
gap> Z6 := HomalgRingOfIntegers()/6;
Z/( 6 )
gap> Z4:= HomalgRingOfIntegers()/4;
Z/( 4 )
gap> IsZero(ZZ);
false
gap> ContainsAField(ZZ);ContainsAField(F2);
false
true
gap> IsRationalsForHomalg(ZZ);IsRationalsForHomalg(F2);
false
false
gap> IsFieldForHomalg(ZZ);IsFieldForHomalg(F2);IsFieldForHomalg(Z6);IsFieldForHomalg(Z4);
false
true
false
false
gap> IsDivisionRingForHomalg(ZZ);IsDivisionRingForHomalg(F2);IsDivisionRingForHomalg(Z6);
false
true
false
gap> IsResidueClassRingOfTheIntegers(ZZ);IsResidueClassRingOfTheIntegers(F2);IsResidueClassRingOfTheIntegers(Z6);IsResidueClassRingOfTheIntegers(Z4);
true
true
true
true
gap> IsBezoutRing(ZZ);
true
gap> IsIntegrallyClosedDomain(ZZ);
true
gap> IsUniqueFactorizationDomain(ZZ);IsUniqueFactorizationDomain(F2);
true
true
gap> IsKaplanskyHermite(ZZ);
true
gap> IsDedekindDomain(ZZ);IsDedekindDomain(F2);IsDedekindDomain(Z6);
true
true
false=>主理想环PIR和主理想整环PID是不同的
每个主理想整环PID都是戴德金整环。
代数数论(algebraic number theory)中的最基本事实是:
一个代数数域K中的代数整数全体(称为K的整数环)/满足理想唯一分解条件的整环是一个戴德金整环(Dedekind Domain)[是整数环Z的弱抽象,是整环的强抽象]。
每个理想可以唯一表示为素理想的乘积。
理想全体是素理想生成的乘法半群,其分式理想全体是一个乘法群,称为K的理想群。
正是这种“理想的唯一素分解”可部分弥补“复数一般不能唯一素因子分解”的不足,在历史上使代数数论发展起来。
理想的唯一分解定理:代数整数环中每一个非平凡理想都可以唯一分解为有限多个素理想的乘积。
gap> IsIntegralDomain(ZZ);IsIntegralDomain(F2);IsIntegralDomain(Z6);
true
true
false
gap> IsNoetherian(ZZ);IsNoetherian(F2);IsNoetherian(Z6);
true
true
true=>诺特环不一定要求是整环
交换代数中的希尔伯特基定理(1888年):若R为诺特环,则R[x]亦然。
[一个系数环上的任何多个变量的多项式所成的环,当这系数的环有一个单位元素和一组有限基时,这多项式环本身也有一组有限基。]
gap> IsLeftNoetherian(ZZ);IsLeftNoetherian(Z6);
true
true
gap> IsRightNoetherian(ZZ);IsRightNoetherian(Z6);
true
true
gap> IsArtinian(ZZ);IsArtinian(F2);
false
整数环是非阿廷环的诺特环
true
gap> IsLeftArtinian(ZZ);
false
gap> IsRightArtinian(ZZ);
false
gap> IsPrincipalIdealRing(ZZ);IsPrincipalIdealRing(F2);IsPrincipalIdealRing(Z6);
true
true
true
证明:整数环Z的每个理想都是主理想。
证明:模m剩余类环的每个理想都是主理想。=>主理想环PIR不一定要求是整环
gap> IsLeftPrincipalIdealRing(ZZ);
true
gap> IsRightPrincipalIdealRing(ZZ);
true
gap> IsRegular(ZZ);IsRegular(F2);
true
true
冯·诺伊曼引入的正则环(regular ring)->戴德金环
同调代数http://www.docin/p-67295980.html
gap> LoadPackage("RingsForHomalg");
true
gap> ZZ:=HomalgRingOfIntegers();
Z
gap> M := HomalgMatrix( "[ 2, 3, 4, 5, 6, 7 ]", 2, 3, ZZ );
<A 2 x 3 matrix over an internal ring>
gap> LoadPackage("Modules");
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
Loading Modules 2015.02.10 (A homalg based package for the Abelian category of finitely presented modules over computable rings)
by Thomas Bächler (http://wwwb.math.rwth-aachen.de/~thomas/),
Mohamed Barakat (http://www.mathematik.uni-kl.de/~barakat/),
Florian Diebold (),
Sebastian Gutsche (http://wwwb.math.rwth-aachen.de/~gutsche/), and
Markus Lange-Hegermann (http://wwwb.math.rwth-aachen.de/~markus/).
Homepage: http://homalg.math.rwth-aachen.de/index.php/core-packages/modules
─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
true
gap> M := LeftPresentation( M );
<A non-torsion left module presented by 2 relations for 3 generators>
gap> Display( M );
[ [ 2, 3, 4 ],
[ 5, 6, 7 ] ] Cokernel of the map Z^(1x2) --> Z^(1x3), currently represented by the above matrix
gap> N := TorsionObject( M );
<A cyclic torsion left module presented by yet unknown relations for a cyclic generator>
gap> iota := TorsionObjectEmb( M );
<A monomorphism of left modules>
gap> psi := Ext( 1, iota, N );
<A homomorphism of right modules>
gap> ByASmallerPresentation( psi );
<A non-zero homomorphism of right modules>
gap> Display( psi );
[ [ 2 ] ] the map is currently represented by the above 1 x 1 matrix
gap> extNN := Range( psi );
<A non-zero cyclic torsion right module on a cyclic generator satisfying 1 relation>
gap> IsIdenticalObj( extNN, Ext( 1, N, N ) );
true
gap> extMN := Source( psi );
<A non-zero cyclic torsion right module on a cyclic generator satisfying 1 relation>
gap> IsIdenticalObj( extMN, Ext( 1, M, N ) );
true
gap> Display( extNN );
Z/< 3 >
gap> Display( extMN );
Z/< 3 >
F:\hxh1\MathTool\有限群\G60
定理:13种60阶群与它们的群元阶的分布一一对应[ 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 ]
Group GAP4(60,1) [C5 x (C3 : C4)]1,1,2,6,4,2,4,0,8,24,8,0,
Group GAP4(60,2) [C3 x (C5 : C4)] 1,1,2,10,4,2,4,20,8,0,8,0,
Group GAP4(60,3) [C15 : C4] 1,1,2,30,4,2,4,0,8,0,8,0,
gap> IdGroup(QuaternionGroup(60));
[ 60, 3 ]
Group GAP4(60,4) [C60] 1,1,2,2,4,2,4,4,8,8,8,16,
gap> IdGroup(CyclicGroup(60));
[ 60, 4 ]
Group GAP4(60,5) [A5] 1,15,20,0,24,0,0,0,0,0,0,0,
60阶群PSL(2,5)同构于60阶群A_5。
GL(2,4)是(16-1)(16-4)=180阶群
GL(2,5)是(25-1)(25-5)=480阶群,SL(2,5)是480/4=120阶群,PSL(2,5)是120/2=60阶群。
gap> IdGroup(Group((1,2,3,4,5),(1,3,2)));
[ 60, 5 ]
gap> IdGroup(Group((1,2,3,4,5),(1,2)(3,4)));
[ 60, 5 ]
gap> IdGroup(Group((3,6)(4,5),(1,2,3)(4,6,5)));
[ 60, 5 ]
gap> IdGroup(Group((1,2)(3,4),(1,3,5)));
[ 60, 5 ]
gap> G:=SmallGroup(6,2);
<pc group of size 6 with 2 generators>
gap> i:=IsomorphismPermGroup(G);
[ f1, f2^2 ] -> [ (1,2), (3,4,5) ]
gap> Image(i,G);
Group([ (1,2), (3,4,5) ])
gap> Elements(Image(i,G));
[ (), (3,4,5), (3,5,4), (1,2), (1,2)(3,4,5), (1,2)(3,5,4) ]
Group GAP4(60,6) [C3 x (C5 : C4)] 1,5,2,10,4,10,0,20,8,0,0,0,
Group GAP4(60,7) [C15 : C4] 1,5,2,30,4,10,0,0,8,0,0,0,
Group GAP4(60,8) [S3 x D10] 1,23,2,0,4,10,12,0,8,0,0,0,
Group GAP4(60,9) [C5 x A4] 1,3,8,0,4,0,12,0,32,0,0,0,
Group GAP4(60,10) [C6 x D10] 1,11,2,0,4,22,4,0,8,0,8,0,
Group GAP4(60,11) [C10 x S3] 1,7,2,0,4,2,28,0,8,0,8,0,
gap> IdGroup(DirectProduct(CyclicGroup(10),SymmetricGroup(3)));
[ 60, 11 ]
Group GAP4(60,12) [D60] 1,31,2,0,4,2,4,0,8,0,8,0,
第13种60阶群:C_15×C_2×C_2
gap> G:=DirectProduct(CyclicGroup(30),CyclicGroup(2));IdGroup(G);L:=List(Elements(G),Order);M:=[1,2,3,4,5,6,10,12,15,20,30,60];for i in M do Print(Size(Positions(L,i)),","); od;
<pc group of size 60 with 4 generators>
[ 60, 13 ]
[ 1, 30, 15, 5, 2, 10, 30, 30, 15, 15, 30, 5, 10, 6, 10, 10, 30, 30, 3, 30, 15, 30, 5, 10, 30, 6, 2, 10, 30, 30, 15,
6, 3, 30, 5, 10, 30, 30, 10, 2, 6, 30, 15, 30, 15, 6, 10, 30, 30, 10, 10, 6, 15, 30, 30, 30, 30, 10, 30, 30 ]
[ 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 ]
1,3,2,0,4,6,12,0,8,0,24,0,
F:\hxh1\MathTool\有限群\G36
gap> IdGroup(QuaternionGroup(36));
[ 36, 1 ]
gap> IdGroup(Group((1,2,3,4,5,6,7,8,9),(10,11,12,13)));
[ 36, 2 ]
gap> IdGroup(Group((1,2,5)(7,8,9),(1,3,5)));
[ 36, 11 ]
gap> IdGroup(Group((3,5,14),(1,3)(2,6,8)(5,14)));
[ 36, 11 ]
gap> IdGroup(Group((1,2)(4,5),(3,5)(7,9,8)));
[ 36, 12 ]
gap> IdGroup(Group((2,8,6)(7,9),(1,3)(5,7,9)));
[ 36, 12 ]
gap> IdGroup(Group((2,8)(9,10,11),(1,6)(3,8)));
[ 36, 12 ]
gap> IdGroup(Group((2,8)(9,10,11),(1,5)(3,8)));
[ 36, 12 ]
gap> IdGroup(Group((2,8)(9,10,18),(1,5)(13,15,17)));
[ 36, 14 ]
F:\hxh1\MathTool\有限群\G24
定理:15种24阶群与它们的群元阶的分布一一对应[ 1, 2, 3, 4, 6, 8, 12, 24 ]
Group GAP4(24,1) [C3 : C8] 1,1,2,2,2,12,4,0,
Group GAP4(24,2) [C24] 1,1,2,2,2,4,4,8,
Group GAP4(24,3) [SL(2,3)] 1,1,8,6,8,0,0,0,
48个可逆的F_3上的2阶方阵构成一般线性群GL(2,3)。----SL(2,3)是24阶群,GL(2,3)是48阶群
GAP4[48,29]=GL(2,3)是(9-1)(9-3)=48阶群
Group GAP4(24,4) [C3 : Q8] 1,1,2,14,2,0,4,0,
gap> IdGroup(QuaternionGroup(24));
[ 24, 4 ]
Group GAP4(24,5) [C4 x S3] 1,7,2,8,2,0,4,0,
Group GAP4(24,6) [D24] 1,13,2,2,2,0,4,0,
Group GAP4(24,7) [C2 x (C3 : C4)] 1,3,2,12,6,0,0,0,
Group GAP4(24,8) [(C6 x C2) : C2] 1,9,2,6,6,0,0,0,
Group GAP4(24,9) [C12 x C2] 1,3,2,4,6,0,8,0,
Group GAP4(24,10) [C3 x D8] 1,5,2,2,10,0,4,0,
Group GAP4(24,11) [C3 x Q8] 1,1,2,6,2,0,12,0,
Group GAP4(24,12) [S4] 1,9,8,6,0,0,0,0,
Group GAP4(24,13) [C2 x A4] 1,7,8,0,8,0,0,0,
Group GAP4(24,14) [C2 x C2 x S3] 1,15,2,0,6,0,0,0,
Group GAP4(24,15) [C6 x C2 x C2]1,7,2,0,14,0,0,0,
gap> IdGroup(Group((1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24)));
[ 24, 2 ]
gap> IdGroup(Group((1,2,3)(4,6,5),(2,5,7)(3,8,6)));
[ 24, 3 ]
gap> IdGroup(Group((1,2,4,3)(5,6),(5,7)));
[ 24, 5 ]
gap> IdGroup(Group((2,3),(1,2)(5,6,7,8)));
[ 24, 5 ]
gap> IdGroup(Group((2,4)(6,7)(9,10),(1,2,3,4)(6,7)(8,9,10)(11,12)));
[ 24, 6 ]
gap> IdGroup(Group((2,4)(6,7)(9,10),(1,2)(3,4)(6,7,8)(11,12)));
[ 24, 8 ]
gap> IdGroup(Group((1,2,3,4),(1,4)(2,3)(5,6,7)));
[ 24, 10 ]
gap> IdGroup(SymmetricGroup(4));
[ 24, 12 ]
验证:S_4共有4!个元素,可由它的5个对换生成:
gap> IdGroup(SymmetricGroup(4))=Group((1,2),(1,3),(1,4),(2,4),(3,4));
true
gap> IdGroup(Group((1,2),(1,3),(1,4),(2,4),(3,4)));
[ 24, 12 ]
gap> IdGroup(Group((2,4,3),(1,2,3,4)));
[ 24, 12 ]
gap> IdGroup(Group((1,2,3,5),(2,3)));
[ 24, 12 ]
gap> IdGroup(Group((4,5),(2,3,4)));
[ 24, 12 ]
gap> IdGroup(Group((1,4,6,5),(1,3,4)(2,5,6)));
[ 24, 12 ]
gap> IdGroup(Group((1,7,4,10),(1,10)));
[ 24, 12 ]
gap> IdGroup(Group((1,6,4,2,5,3),(5,6)));
[ 24, 13 ]
gap> IdGroup(Group((1,5)(3,8,9,4,6,10),(1,5)(9,10)));
[ 24, 13 ]
F:\hxh1\MathTool\有限群\G4
gap> IdGroup(Group((1,2,3,4)));
[ 4, 1 ]
gap> IdGroup(Group((3,4),(1,2)));
[ 4, 2 ]
F:\hxh1\MathTool\有限群\G6
gap> IdGroup(Group((2,4),(4,5)));
[ 6, 1 ]
gap> IdGroup(Group((1,2,3),(5,6)(7,8)(9,10)));
[ 6, 2 ]
gap> IdGroup(Group((1,2,3,4,5,6)));
[ 6, 2 ]
F:\hxh1\MathTool\有限群\G8
gap> IdGroup(Group((1,2),(3,4,5,6)));
[ 8, 2 ]
gap> IdGroup(Group((1,2,3,4),(5,6)));
[ 8, 2 ]
gap> IdGroup(Group((1,2,3,4),(5,6),(1,3)(2,4),(1,3)(2,4)(5,6),(1,4,3,2),(1,4,3,2)(5,6),(1,2,3,4)(5,6)));
[ 8, 2 ]
gap> IdGroup(Group((1,2,3,4),(1,4,3,2)(5,7)(6,8)));
[ 8, 2 ]
gap> IdGroup(Group((1,2)(3,4)(5,6)(7,8),(1,5,2,6)(3,7,4,8),(1,7,2,8)(3,5,4,6)));
[ 8, 2 ]
gap> IdGroup(Group((1,2,3,4),(1,3)));
[ 8, 3 ]
gap> IdGroup(Group((1,2,3,4),(2,4)(5,6)));
[ 8, 3 ]
gap> IdGroup(Group((1,3)(2,4)(6,7),(2,3)));
[ 8, 3 ]
gap> IdGroup(Group((2,4)(6,7)(9,10),(1,2,3,4)(6,7)(11,12)));
[ 8, 3 ]F:\hxh1\MathTool\有限群\G9
gap> IdGroup(Group((1,2,3),(4,5,6)));
[ 9, 2 ]
gap> IdGroup(Group((1,2,3),(4,5,6),(1,3,2),(4,6,5),(1,2,3)(4,5,6),(1,2,3)(4,6,5),(1,3,2)(4,6,5),(1,3,2)(4,5,6)));
[ 9, 2 ]
F:\hxh1\MathTool\有限群\G12
gap> IdGroup(Group((1,6)(4,5),(1,2,6,5,3,4)));
[ 12, 4 ]
gap> IdGroup(Group((1,3,5)(4,6),(1,5)));
[ 12, 4 ]
F:\hxh1\MathTool\有限群\Sn的子群
gap> G:=SmallGroup(8,1);
<pc group of size 8 with 3 generators>
gap> i:=IsomorphismPermGroup(G);
[ f1*f2 ] -> [ (1,2,3,4,5,6,7,8) ]
gap> Image(i,G);
Group([ (1,2,3,4,5,6,7,8) ])
gap> Elements(Image(i,G));
[ (), (1,2,3,4,5,6,7,8), (1,3,5,7)(2,4,6,8), (1,4,7,2,5,8,3,6), (1,5)(2,6)(3,7)(4,8), (1,6,3,8,5,2,7,4),
(1,7,5,3)(2,8,6,4), (1,8,7,6,5,4,3,2) ]
gap> IdGroup(Group((1,2,3,4,5,6,7,8)));
[ 8, 1 ]
gap> IdGroup(Group((1,5,3,7,2,6,4,8),(1,3,2,4)(5,7,6,8),(1,2)(3,4)(5,6)(7,8)));
[ 8, 1 ]
gap> IdGroup(Group((1,2),(3,4,5,6)));
[ 8, 2 ]
gap> IdGroup(Group((2,4)(6,7)(9,10),(1,2,3,4)(6,7)(11,12)));
gap> IdGroup(DihedralGroup(8));
[ 8, 3 ]
gap> IdGroup(DihedralGroup(IsPermGroup,8));
Group([(1,2,3,4),(2,4)])
[ 8, 3 ]
gap> IdGroup(Group((1,3)(2,4),(1,4)(2,3),(3,4)));
[ 8, 3 ]
gap> IdGroup(Group((1,5,2,6)(3,8,4,7),(1,3,2,4)(5,7,6,8),(1,2)(3,4)(5,6)(7,8)));
[ 8, 4 ]
gap> IdGroup(QuaternionGroup(8));
[ 8, 4 ]
gap> IdGroup(ElementaryAbelianGroup(8));
[ 8, 5 ]
gap> IdGroup(Group((1,2),(3,4),(5,6)));
[ 8, 5 ]
gap> IdGroup(Group((1,2),(3,4),(5,6),(1,2)(3,4),(1,2)(5,6),(3,4)(5,6),(1,2)(3,4)(5,6)));
[ 8, 5 ]
gap> IdGroup(Group((1,2,3)(4,5),(4,5)(7,8)));
[ 12, 5 ]
gap> IdGroup(Group((1,2,3)(4,5)(6,7),(1,3,2)(6,7)));
[ 12, 5 ]
gap> IdGroup(Group((1,2,3)(4,5)(6,7),(1,3,2)(6,7),(1,3,2)));
[ 12, 5 ]
gap> IdGroup(Group((1,2,3,4,5,6)(7,8,9,10,11,12),(1,7,4,10)(2,12,5,9)(3,11,6,8)));
[ 12, 1 ]
gap> IdGroup(Group((1,2,3,4,5,6)(7,8,9,10,11,12),(1,7,4,10)(2,12,5,9)(3,11,6,8),(1,6,5,4,3,2)(7,12,11,10,9,8),(1,3,5)(2,4,6)(7,9,11)(8,10,12),(1,4)(2,5)(3,6)(7,10)(8,11)(9,12)));
[ 12, 1 ]
gap> IdGroup(QuaternionGroup(12));
[ 12, 1 ]
gap> IdGroup(Group((1,2,3,4,5,6,7,8,9,10,11,12)));
[ 12, 2 ]
gap> IdGroup(Group((),(1,2,3),(1,3,2),(1,2,4),(1,4,2),(1,3,4),(1,4,3),(2,3,4),(2,4,3),(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)));
[ 12, 3 ]
gap> IdGroup(Group((5,6),(1,2,3)(4,5)));
[ 18, 3 ]
gap> IdGroup(Group((3,6)(4,5),(2,4,5),(1,3)(4,5)));
[ 18, 4 ]
gap> IdGroup(QuaternionGroup(20));
[ 20, 1 ]
gap> IdGroup(Group((2,3)(4,5),(1,2,3,4)));
[ 20, 3 ]
http://groupprops.subwiki/wiki/GAP:IdGroup
gap> IdGroup(CyclicGroup(6));
[ 6, 2 ]
gap> IdGroup(SL(2,5));
[ 120, 5 ]
gap> IdGroup(SL(2,5))[2];
5
gap> IdGroup(SmallGroup(24,7));
[ 24, 7 ]
gap> G := SymmetricGroup(4);
Sym( [ 1 .. 4 ] )
gap> H := DirectProduct(G,G);
Group([ (1,2,3,4), (1,2), (5,6,7,8), (5,6) ])
gap> IdGroup(H);
[ 576, 8653 ]
gap> G:=SmallGroup(6,2);
<pc group of size 6 with 2 generators>
gap> List(NormalSubgroups(G),IdGroup);
[ [ 6, 2 ], [ 2, 1 ], [ 3, 1 ], [ 1, 1 ] ]
gap> V4:=Group([(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)]);
Group([ (1,2)(3,4), (1,3)(2,4), (1,4)(2,3) ])
gap> IdGroup(V4);
[ 4, 2 ]
群的置换表示和GAP ID
3,9,12,13?
gap> IdGroup(Group([(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16)]));[ 16, 1 ]
gap> IdGroup(Group([(1,2,3,4),(5,6,7,8)]));[ 16, 2 ]
gap> IdGroup(Group((1,7,4,10),(5,6,8,9)));
[ 16, 2 ]
gap> IdGroup(Group([(1,2,3,4),(1,3)(5,6,7,8)]));[ 16, 4 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(9,10)]));[ 16, 5 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(1,5)(3,7)]));[ 16, 6 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(1,7)(3,5)(2,6)]));[ 16, 7 ]
gap> IdGroup(Group([(1,2,3,4,5,6,7,8),(1,3)(5,7)(2,6)]));[ 16, 8 ]
gap> IdGroup(Group([(1,2,3,4),(5,6),(7,8)]));[ 16, 10 ]
gap> IdGroup(Group([(1,2,3,4),(1,3),(5,6)]));[ 16, 11 ]
gap> IdGroup(Group([(1,2),(3,4),(5,6),(7,8)]));[ 16, 14 ]
gap> IdGroup(ElementaryAbelianGroup(16));
[ 16, 14 ]
gap> IdGroup(Group((1,5)(2,6)(3,4,8,9)(7,10),(1,6)));
[ 16, 3 ]
两个生成元分别是4阶元和2阶元
gap> G:=SmallGroup(16,3);
<pc group of size 16 with 4 generators>
gap> i:=IsomorphismPermGroup(G);
<action isomorphism>
gap> Image(i,G);
Group([ (1,2,5,8)(3,12,10,16)(4,7,11,14)(6,15,13,9), (1,3)(2,6)(4,9)(5,10)(7,12)(8,13)(11,15)(14,16), (1,4)(2,7)(3,9)
(5,11)(6,12)(8,14)(10,15)(13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16) ])
gap> Elements(Image(i,G));
[ (), (1,2,5,8)(3,12,10,16)(4,7,11,14)(6,15,13,9), (1,3)(2,6)(4,9)(5,10)(7,12)(8,13)(11,15)(14,16),
(1,4)(2,7)(3,9)(5,11)(6,12)(8,14)(10,15)(13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16),
(1,6,11,16)(2,10,14,9)(3,7,15,8)(4,12,5,13), (1,7,5,14)(2,11,8,4)(3,6,10,13)(9,12,15,16),
(1,8,5,2)(3,16,10,12)(4,14,11,7)(6,9,13,15), (1,9)(2,12)(3,4)(5,15)(6,7)(8,16)(10,11)(13,14),
(1,10)(2,13)(3,5)(4,15)(6,8)(7,16)(9,11)(12,14), (1,11)(2,14)(3,15)(4,5)(6,16)(7,8)(9,10)(12,13),
(1,12,11,13)(2,15,14,3)(4,6,5,16)(7,10,8,9), (1,13,11,12)(2,3,14,15)(4,16,5,6)(7,9,8,10),
(1,14,5,7)(2,4,8,11)(3,13,10,6)(9,16,15,12), (1,15)(2,16)(3,11)(4,10)(5,9)(6,14)(7,13)(8,12),
(1,16,11,6)(2,9,14,10)(3,8,15,7)(4,13,5,12) ]
gap> IdGroup(QuaternionGroup(16));
[ 16, 9 ]
gap> G:=SmallGroup(16,9);
<pc group of size 16 with 4 generators>
gap> i:=IsomorphismPermGroup(G);
<action isomorphism>
gap> Image(i,G);
Group([ (1,2,5,8)(3,12,10,16)(4,14,11,7)(6,15,13,9), (1,3,5,10)(2,6,8,13)(4,15,11,9)(7,16,14,12), (1,4,5,11)(2,7,8,14)
(3,9,10,15)(6,12,13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16) ])
gap> Elements(Image(i,G));
[ (), (1,2,5,8)(3,12,10,16)(4,14,11,7)(6,15,13,9), (1,3,5,10)(2,6,8,13)(4,15,11,9)(7,16,14,12),
(1,4,5,11)(2,7,8,14)(3,9,10,15)(6,12,13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16),
(1,6,11,16,5,13,4,12)(2,10,14,9,8,3,7,15), (1,7,5,14)(2,11,8,4)(3,13,10,6)(9,12,15,16),
(1,8,5,2)(3,16,10,12)(4,7,11,14)(6,9,13,15), (1,9,5,15)(2,12,8,16)(3,11,10,4)(6,14,13,7),
(1,10,5,3)(2,13,8,6)(4,9,11,15)(7,12,14,16), (1,11,5,4)(2,14,8,7)(3,15,10,9)(6,16,13,12),
(1,12,4,13,5,16,11,6)(2,15,7,3,8,9,14,10), (1,13,11,12,5,6,4,16)(2,3,14,15,8,10,7,9),
(1,14,5,7)(2,4,8,11)(3,6,10,13)(9,16,15,12), (1,15,5,9)(2,16,8,12)(3,4,10,11)(6,7,13,14),
(1,16,4,6,5,12,11,13)(2,9,7,10,8,15,14,3) ]
gap> G:=SmallGroup(16,12);
<pc group of size 16 with 4 generators>
gap> i:=IsomorphismPermGroup(G);
<action isomorphism>
gap> Image(i,G);
Group([ (1,2,5,8)(3,13,10,6)(4,7,11,14)(9,16,15,12), (1,3,5,10)(2,6,8,13)(4,9,11,15)(7,12,14,16), (1,4)(2,7)(3,9)
(5,11)(6,12)(8,14)(10,15)(13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16) ])
gap> Elements(Image(i,G));
[ (), (1,2,5,8)(3,13,10,6)(4,7,11,14)(9,16,15,12), (1,3,5,10)(2,6,8,13)(4,9,11,15)(7,12,14,16),
(1,4)(2,7)(3,9)(5,11)(6,12)(8,14)(10,15)(13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16),
(1,6,5,13)(2,10,8,3)(4,12,11,16)(7,15,14,9), (1,7,5,14)(2,11,8,4)(3,16,10,12)(6,9,13,15),
(1,8,5,2)(3,6,10,13)(4,14,11,7)(9,12,15,16), (1,9,5,15)(2,12,8,16)(3,11,10,4)(6,14,13,7),
(1,10,5,3)(2,13,8,6)(4,15,11,9)(7,16,14,12), (1,11)(2,14)(3,15)(4,5)(6,16)(7,8)(9,10)(12,13),
(1,12,5,16)(2,15,8,9)(3,7,10,14)(4,6,11,13), (1,13,5,6)(2,3,8,10)(4,16,11,12)(7,9,14,15),
(1,14,5,7)(2,4,8,11)(3,12,10,16)(6,15,13,9), (1,15,5,9)(2,16,8,12)(3,4,10,11)(6,7,13,14),
(1,16,5,12)(2,9,8,15)(3,14,10,7)(4,13,11,6) ]
gap> G:=SmallGroup(16,13);
<pc group of size 16 with 4 generators>
gap> i:=IsomorphismPermGroup(G);
<action isomorphism>
gap> Image(i,G);
Group([ (1,2)(3,13)(4,7)(5,8)(6,10)(9,16)(11,14)(12,15), (1,3)(2,6)(4,9)(5,10)(7,12)(8,13)(11,15)(14,16), (1,4,5,11)
(2,7,8,14)(3,9,10,15)(6,12,13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16) ])
gap> Elements(Image(i,G));
[ (), (1,2)(3,13)(4,7)(5,8)(6,10)(9,16)(11,14)(12,15), (1,3)(2,6)(4,9)(5,10)(7,12)(8,13)(11,15)(14,16),
(1,4,5,11)(2,7,8,14)(3,9,10,15)(6,12,13,16), (1,5)(2,8)(3,10)(4,11)(6,13)(7,14)(9,15)(12,16),
(1,6,5,13)(2,3,8,10)(4,12,11,16)(7,9,14,15), (1,7,5,14)(2,4,8,11)(3,16,10,12)(6,15,13,9),
(1,8)(2,5)(3,6)(4,14)(7,11)(9,12)(10,13)(15,16), (1,9,5,15)(2,12,8,16)(3,4,10,11)(6,7,13,14),
(1,10)(2,13)(3,5)(4,15)(6,8)(7,16)(9,11)(12,14), (1,11,5,4)(2,14,8,7)(3,15,10,9)(6,16,13,12),
(1,12)(2,9)(3,14)(4,13)(5,16)(6,11)(7,10)(8,15), (1,13,5,6)(2,10,8,3)(4,16,11,12)(7,15,14,9),
(1,14,5,7)(2,11,8,4)(3,12,10,16)(6,9,13,15), (1,15,5,9)(2,16,8,12)(3,11,10,4)(6,14,13,7),
(1,16)(2,15)(3,7)(4,6)(5,12)(8,9)(10,14)(11,13) ]
S_4、S_5的子群
http://www.docin/p-670969262.html
董井成:GAP在近世代数教学中的应用
GAP是一款绿色软件,不需要安装,双击C:\gap4r7\bin下的批处理文件gap.bat即可启动软件,显示输入提示符gap>
。GAP的界面类似DOS。GAP语句以分号结尾,不能省略。
群的最高阶可以达到几万。
循环群、对称群、二面体群分别用函数
gap> IdGroup(CyclicGroup(3));
[ 3, 1 ]
gap> IdGroup(Group((1,2,3),(1,2,4),(1,3,4)));
[ 12, 3 ]
gap>IdGroup(Group((1,2,3),(1,3,2),(1,2,4),(1,4,2),(1,3,4),(1,4,3),(2,3,4),(2,4,3),(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)));
[ 12, 3 ]
偶置换:逆序数的个数是偶数。
奇置换:逆序数的个数是奇数。
(1)=(2)=(3)=(4)=I
8个长度3的轮换:(123),(124),(134)
长度4的轮换:
2个对换的乘积:
20151008:半直积的例子
gap> C3:=CyclicGroup(IsPermGroup,3);;C7:=CyclicGroup(IsPermGroup,7);;A:=AutomorphismGroup(C7);;elts := Elements(A);sigma := elts[4];sigma^3;map := GroupHomomorphismByImages(C3, A, GeneratorsOfGroup(C3), [sigma]);SDP := SemidirectProduct(C3, map, C7);IdGroup(SDP);List(elts,Order);IdGroup(DirectProduct( C3, C7 ));
[ [ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ], [ (1,2,3,4,5,6,7) ] -> [ (1,3,5,7,2,4,6) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,4,7,3,6,2,5) ], [ (1,2,3,4,5,6,7) ] -> [ (1,5,2,6,3,7,4) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,6,4,2,7,5,3) ], [ (1,2,3,4,5,6,7) ] -> [ (1,7,6,5,4,3,2) ] ]
[ (1,2,3,4,5,6,7) ] -> [ (1,5,2,6,3,7,4) ]
[ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ]
[ (1,2,3) ] -> [ [ (1,2,3,4,5,6,7) ] -> [ (1,5,2,6,3,7,4) ] ]
Group([ (4,5,6,7,8,9,10), (1,2,3)(5,8,6)(7,9,10) ])
[ 21, 1 ]
[ 1, 3, 6, 3, 6, 2 ]
[ 21, 2 ]
gap> C3:=CyclicGroup(IsPermGroup,3);;C7:=CyclicGroup(IsPermGroup,7);;A:=AutomorphismGroup(C7);;elts := Elements(A);sigma := elts[2];sigma^3;map := GroupHomomorphismByImages(C3, A, GeneratorsOfGroup(C3), [sigma]);SDP := SemidirectProduct(C3, map, C7);IdGroup(SDP);List(elts,Order);IdGroup(DirectProduct( C3, C7 ));
[ [ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ], [ (1,2,3,4,5,6,7) ] -> [ (1,3,5,7,2,4,6) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,4,7,3,6,2,5) ], [ (1,2,3,4,5,6,7) ] -> [ (1,5,2,6,3,7,4) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,6,4,2,7,5,3) ], [ (1,2,3,4,5,6,7) ] -> [ (1,7,6,5,4,3,2) ] ]
[ (1,2,3,4,5,6,7) ] -> [ (1,3,5,7,2,4,6) ]
[ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ]
[ (1,2,3) ] -> [ [ (1,2,3,4,5,6,7) ] -> [ (1,3,5,7,2,4,6) ] ]
Group([ (4,5,6,7,8,9,10), (1,2,3)(5,6,8)(7,10,9) ])
[ 21, 1 ]
[ 1, 3, 6, 3, 6, 2 ]
[ 21, 2 ]
gap> C3:=CyclicGroup(IsPermGroup,3);;C7:=CyclicGroup(IsPermGroup,7);;A:=AutomorphismGroup(C7);;elts := Elements(A);sigma := elts[1];sigma^3;map := GroupHomomorphismByImages(C3, A, GeneratorsOfGroup(C3), [sigma]);SDP := SemidirectProduct(C3, map, C7);IdGroup(SDP);List(elts,Order);IdGroup(DirectProduct( C3, C7 ));
[ [ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ], [ (1,2,3,4,5,6,7) ] -> [ (1,3,5,7,2,4,6) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,4,7,3,6,2,5) ], [ (1,2,3,4,5,6,7) ] -> [ (1,5,2,6,3,7,4) ],
[ (1,2,3,4,5,6,7) ] -> [ (1,6,4,2,7,5,3) ], [ (1,2,3,4,5,6,7) ] -> [ (1,7,6,5,4,3,2) ] ]
[ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ]
[ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ]
[ (1,2,3) ] -> [ [ (1,2,3,4,5,6,7) ] -> [ (1,2,3,4,5,6,7) ] ]
Group([ (4,5,6,7,8,9,10), (1,2,3) ])
[ 21, 2 ]
[ 1, 3, 6, 3, 6, 2 ]
[ 21, 2 ]
gap> C8:=CyclicGroup(IsPermGroup,8);;C3:=CyclicGroup(IsPermGroup,3);;A:=AutomorphismGroup(C3);;elts := Elements(A);sigma := elts[1];sigma^2;map := GroupHomomorphismByImages(C8, A, GeneratorsOfGroup(C8), [sigma]);SDP := SemidirectProduct(C8, map, C3);IdGroup(SDP);List(elts,Order);IdGroup(DirectProduct( C8, C3 ));
[ [ (1,2,3) ] -> [ (1,2,3) ], [ (1,2,3) ] -> [ (1,3,2) ] ]
[ (1,2,3) ] -> [ (1,2,3) ]
[ (1,2,3) ] -> [ (1,2,3) ]
[ (1,2,3,4,5,6,7,8) ] -> [ [ (1,2,3) ] -> [ (1,2,3) ] ]
Group([ (9,10,11), (1,2,3,4,5,6,7,8) ])
[ 24, 2 ]
[ 1, 2 ]
[ 24, 2 ]
gap> C8:=CyclicGroup(IsPermGroup,8);;C3:=CyclicGroup(IsPermGroup,3);;A:=AutomorphismGroup(C3);;elts := Elements(A);sigma := elts[2];sigma^2;map := GroupHomomorphismByImages(C8, A, GeneratorsOfGroup(C8), [sigma]);SDP := SemidirectProduct(C8, map, C3);IdGroup(SDP);List(elts,Order);IdGroup(DirectProduct( C8, C3 ));
[ [ (1,2,3) ] -> [ (1,2,3) ], [ (1,2,3) ] -> [ (1,3,2) ] ]
[ (1,2,3) ] -> [ (1,3,2) ]
[ (1,2,3) ] -> [ (1,2,3) ]
[ (1,2,3,4,5,6,7,8) ] -> [ [ (1,2,3) ] -> [ (1,3,2) ] ]
Group([ (9,10,11), (1,2,3,4,5,6,7,8)(10,11) ])
[ 24, 1 ]
[ 1, 2 ]
[ 24, 2 ]
20151006:GAP求有限群的共轭类个数以及每个共轭类的长度
gap> G:=SymmetricGroup(4);IdGroup(G);cl:=ConjugacyClasses(G);len:=Size(cl);for i in [1..len] do Print(Size(cl[i]),","); od;Print("\n");for i in [1..len] do Print(IdGroup(Centralizer(cl[i])),","); od;
Sym( [ 1 .. 4 ] )
[ 24, 12 ]
[ ()^G, (1,2)^G, (1,2)(3,4)^G, (1,2,3)^G, (1,2,3,4)^G ]
5
1,6,3,8,6,
[ 24, 12 ],[ 4, 2 ],[ 8, 3 ],[ 3, 1 ],[ 4, 1 ],
gap> G:=SmallGroup(48,11);IdGroup(G);L:=List(ConjugacyClasses(G),Size);len:=Size(L);M:=[1, 2, 3, 4, 6, 8, 12, 16, 24, 48];for i in M do Print(Size(Positions(L,i)),","); od;
<pc group of size 48 with 5 generators>
[ 48, 11 ]
[ 1, 3, 1, 1, 1, 2, 3, 3, 3, 1, 1, 2, 1, 2, 2, 3, 3, 3, 1, 2, 2, 2, 3, 2 ]
24
[ 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 ]
8,8,8,0,0,0,0,0,0,0,
gap> G:=SmallGroup(48,12);IdGroup(G);L:=List(ConjugacyClasses(G),Size);len:=Size(L);M:=[1, 2, 3, 4, 6, 8, 12, 16, 24, 48];for i in M do Print(Size(Positions(L,i)),","); od;
<pc group of size 48 with 5 generators>
[ 48, 12 ]
[ 1, 6, 2, 1, 1, 2, 6, 6, 2, 2, 1, 2, 2, 6, 2, 2, 2, 2 ]
18
[ 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 ]
4,10,0,0,4,0,0,0,0,0,
gap> G:=SmallGroup(48,13);IdGroup(G);L:=List(ConjugacyClasses(G),Size);len:=Size(L);M:=[1, 2, 3, 4, 6, 8, 12, 16, 24, 48];for i in M do Print(Size(Positions(L,i)),","); od;
<pc group of size 48 with 5 generators>
[ 48, 13 ]
[ 1, 6, 2, 1, 1, 2, 6, 6, 2, 2, 1, 2, 2, 6, 2, 2, 2, 2 ]
18
[ 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 ]
4,10,0,0,4,0,0,0,0,0,
gap> G:=SmallGroup(48,34);IdGroup(G);L:=List(ConjugacyClasses(G),Size);len:=Size(L);M:=[1, 2, 3, 4, 6, 8, 12, 16, 24, 48];for i in M do Print(Size(Positions(L,i)),","); od;
<pc group of size 48 with 5 generators>
[ 48, 34 ]
[ 1, 6, 1, 2, 1, 2, 6, 6, 2, 1, 2, 2, 2, 6, 2, 2, 2, 2 ]
18
[ 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 ]
4,10,0,0,4,0,0,0,0,0,
德国数学家弗罗贝尼乌斯(Ferdinand Georg Frobenius,1849.10.26-1917.8.3)曾经提出了一个著名的猜想:共轭类数为n的有限群,在同构意义下是有限的。该猜想最先由E.Landau证明,他给出了具有n个共轭类的有限群的阶的上界,从而肯定了猜想的正确性。
定理(Frobenius猜想):共轭类数为n的有限群,在同构意义下是有限的。
定理:有限群为交换群的充要条件是Con(G)=|G|。
定理:共轭类数为1的有限群,只能是单位元群C_1。共轭类数为2的有限群,只能是2阶循环群C_2。共轭类数为3的有限群,是可解群,是3阶循环群或者6阶群。
gap> Size(ConjugacyClasses(SmallGroup(6,1)));
3
gap> Size(ConjugacyClasses(SmallGroup(6,2)));
6
gap> Size(ConjugacyClasses(SmallGroup(1,1)));
1
gap> Size(ConjugacyClasses(SmallGroup(2,1)));
2
gap> Size(ConjugacyClasses(SmallGroup(3,1)));
3
gap> Size(ConjugacyClasses(SmallGroup(4,1)));
4
gap> Size(ConjugacyClasses(SmallGroup(4,2)));
4
gap> Size(ConjugacyClasses(SmallGroup(5,1)));
5
gap> Size(ConjugacyClasses(SmallGroup(48,11)));
24
gap> Size(ConjugacyClasses(SmallGroup(48,12)));
18
gap> Size(ConjugacyClasses(SmallGroup(48,13)));
18
gap> Size(ConjugacyClasses(SmallGroup(48,34)));
18
gap> IdGroup(AutomorphismGroup(SmallGroup(48,34)));
[ 384, 12882 ]
gap> IdGroup(AutomorphismGroup(SmallGroup(48,11)));
[ 192, 1147 ]
gap> IdGroup(AutomorphismGroup(SmallGroup(48,12)));
[ 96, 230 ]
gap> IdGroup(AutomorphismGroup(SmallGroup(48,13)));
[ 192, 1147 ]
gap> IsNilpotentGroup(SmallGroup(48,12));
false
gap> IsNilpotentGroup(SmallGroup(48,11));
false
gap> IsNilpotentGroup(SmallGroup(48,13));
false
gap> IsNilpotentGroup(SmallGroup(48,34));
false
gap> IsSolvableGroup(SmallGroup(48,12));
true
gap> IsSolvableGroup(SmallGroup(48,11));
true
gap> IsSolvableGroup(SmallGroup(48,13));
true
gap> IsSolvableGroup(SmallGroup(48,34));
true
gap> IsSupersolvableGroup(SmallGroup(48,34));
true
gap> IsSupersolvableGroup(SmallGroup(48,11));
true
gap> IsSupersolvableGroup(SmallGroup(48,12));
true
gap> IsSupersolvableGroup(SmallGroup(48,13));
true
gap> IsAlmostSimpleGroup(SmallGroup(48,13));
false
gap> IsAlmostSimpleGroup(SmallGroup(48,11));
false
gap> IsAlmostSimpleGroup(SmallGroup(48,12));
false
gap> IsAlmostSimpleGroup(SmallGroup(48,34));
false
gap> IsPolycyclicGroup(SmallGroup(48,34));
true
gap> IsPolycyclicGroup(SmallGroup(48,11));
true
gap> IsPolycyclicGroup(SmallGroup(48,12));
true
gap> IsPolycyclicGroup(SmallGroup(48,13));
true
20151003:GAP中计算多项式的伽罗瓦群:
gap> x:=Indeterminate(Rationals);
x
gap> poly:=x^8-2;
x^8-2
gap> g:=TransitiveGroup(Degree(poly),GaloisType(poly));
2D_8(8)=[D(4)]2
gap> IdGroup(g);
[ 16, 8 ]
gap> f1:=x^5-x-1;
x^5-x-1
gap> IdGroup(TransitiveGroup(Degree(f1),GaloisType(f1)));
[ 120, 34 ]
gap> IdGroup(SymmetricGroup(5));
[ 120, 34 ]
这是一个非可解扩张的伽罗瓦扩张:记K是f(x)=x^5-x-1∈Q[x]的分裂域,则Gal(K/Q)=S_5(一种不可解群),所以K/Q是非可解扩张的伽罗瓦扩张。又记作G(x^5-x-1,Q)=S_5。
gap> f2:=x^3-2;
x^3-2
gap> IdGroup(TransitiveGroup(Degree(f2),GaloisType(f2)));
[ 6, 1 ]
gap> e2:=AlgebraicExtension(Rationals,f2);
<algebraic extension over the Rationals of degree 3>
gap> IsAlgebraicExtension(e2);
true
gap> IsField(e2);
true
这是一个非阿贝尔扩张的可解扩张:记K是f(x)=x^3-2∈Q[x]的分裂域,则Gal(K/Q)=S_3(一种非幂零的超可解群),所以K/Q是非阿贝尔扩张的可解扩张。
gap> x:=Indeterminate(Rationals);
x
gap> f4:=x^3+2;
x^3+2
gap> IdGroup(TransitiveGroup(Degree(f4),GaloisType(f4)));
[ 6, 1 ]
这也是一个非阿贝尔扩张的可解扩张:x^3+2在Q上的分裂域是Q(e^(2pii/3),2^(1/3))=Q(r_1,r_2,r_3)。
gap> f3:=x^4-10*x^2+1;
x^4-10*x^2+1
gap> IdGroup(TransitiveGroup(Degree(f3),GaloisType(f3)));
[ 4, 2 ]
这是一个非循环扩张的阿贝尔扩张,例如多项式x^4-10x^2+1=(x^2-5)^2-24有四个根:x_1=sqrt(2)+sqrt(3),x_2=sqrt(2)-sqrt(3),x_3=-sqrt(2)+sqrt(3),x_4=-sqrt(2)-sqrt(3)。伽罗瓦群是Klein四元群(一种非循环的阿贝尔群),所以扩张Q(sqrt(2),sqrt(3))/Q是非循环扩张的阿贝尔扩张。(x^2-2)(x^2-3)在Q上的分裂域是Q(sqrt(2),sqrt(3))=Q(sqrt(2)+sqrt(3))。Q(sqrt(2))/Q是二次扩张,Q(sqrt(2),sqrt(3))/Q(sqrt(2))是二次扩张=>Q(sqrt(2),sqrt(3))/Q是四次扩张。
gap> IdGroup(GaloisGroup(Field(Sqrt(2))));
[ 2, 1 ]
gap> IdGroup(GaloisGroup(Field(Sqrt(-2))));
[ 2, 1 ]
这是二次循环扩张的例子:①Gal(Q(sqrt(2))/Q)=C_2,[Q(sqrt(2)):Q]=|C_2|=2。x^2-2和x^4-4在Q上的分裂域都是Q(sqrt(2)),其伽罗瓦群都是C_2。Q(sqrt(2))/Q是正规域扩张,它包括了x^2-2的所有根。②Gal(Q(sqrt(3))/Q)=C_2,[Q(sqrt(3)):Q]=|C_2|=2。x^2-4x+1在Q上的分裂域是Q=(2+sqrt(3),2-sqrt(3))=Q(sqrt(3)),其伽罗瓦群是C_2。按:Q的以下两个单代数扩域是同构的:Q(sqrt(2))=Q(sqrt(3)),其中同构映射f:a+bsqrt(2)->a+bsqrt(3)。一般地,若g(x)是某域F上的n次不可约多项式,a和b是g(x)的两个根,则F(a)和F(b)是同构的单代数扩域。
这是Gal(Q/Q)=C_1的例子: x^2-4x+4=(x-2)^2和x^2-3x+2=(x-2)(x-1)在Q上的分裂域为Q,其伽罗瓦群是平凡的。
考虑多项式f(x)=x^2+1∈Q[x]
f(x)在C中是分裂的,但它在Q上的分裂域是Q(i)={a+bi|a,b∈Q}
f(x)在R上的分裂域是C。
考虑多项式f(x)=x^2-3∈Q[x]
f(x)在R中是分裂的,但它在Q上的分裂域是Q(sqrt(3))={a+bsqrt(3)|a,b∈Q}(它也等于Q[sqrt(3)])。
gap> x := Indeterminate( Rationals, "x" );
x
gap> f := UnivariatePolynomial( Rationals, [1,0,1] );
x^2+1
gap> L := SplittingField( f );
<algebraic extension over the Rationals of degree 2>
gap> IdGroup(GaloisGroupOnRoots(f));
[ 2, 1 ]
gap> f1 := UnivariatePolynomial( Rationals, [-3,0,1] );
x^2-3
gap> L1 := SplittingField( f1 );
<algebraic extension over the Rationals of degree 2>
gap> IdGroup(GaloisGroupOnRoots(f1));
[ 2, 1 ]
假定F=F_2,α是F[x]中不可约多项式x^2+x+1的一个根,证明F(α)={0,1,α,1+α}是一个含4个元素的域。求多项式x^2+x+1的另一个根。
gap> x:=X(GF(2),"x");
x
gap> f:=x^2+x+1;
x^2+x+Z(2)^0
gap> IsIrreducible(f);
true
gap> F:=AlgebraicExtension(GF(2),f);
<algebra-with-one of dimension 2 over GF(2)>
gap> a:=RootOfDefiningPolynomial(F);
a
gap> a^2;a^3;a^4;
a+Z(2)^0
!Z(2)^0
a
gap> a+a;a+a+a;a+a+a+a;
!0*Z(2)
a
!0*Z(2)
gap> Elements(F);
[ !0*Z(2), a, !Z(2)^0, a+Z(2)^0 ]
gap> Factors(f);
[ x^2+x+Z(2)^0 ]
伽罗瓦域GF(p^m)给出了伽罗瓦群的一个特别简单的例子,这里是把它包含的素域GF(p)作为基域。Gal(GF(p^m)/GF(p))是m阶的循环群。
gap> IdGroup(GaloisGroup(GF(256)));
[ 8, 1 ]
gap> IdGroup(GaloisGroup(AsField(GF(2),GF(256))));
[ 8, 1 ]
gap> IdGroup(GaloisGroup(AsField(GF(4),GF(256))));
[ 4, 1 ]
gap> IdGroup(GaloisGroup(AsField(GF(4),GF(4096))));
[ 6, 2 ]
gap> IdGroup(GaloisGroup ( GF(32)));
[ 5, 1 ]
gap> IdGroup(GaloisGroup ( GF(16)));
[ 4, 1 ]
gap> IdGroup(GaloisGroup ( GF(8)));
[ 3, 1 ]
gap> IdGroup(GaloisGroup ( GF(4)));
[ 2, 1 ]
gap> IdGroup(GaloisGroup ( GF(2)));
[ 1, 1 ]
gap> IdGroup(GaloisGroup(GF(3)));
[ 1, 1 ]
gap> IdGroup(GaloisGroup ( GF(9)));
[ 2, 1 ]
gap> IdGroup(GaloisGroup ( GF(27)));
[ 3, 1 ]
gap> IdGroup(GaloisGroup ( GF(81)));
[ 4, 1 ]
记F=Z_2是含2个元素的域,证明多项式x^2+1在多项式环F[x]中可约,而x^2+x+1在多项式环F[x]中不可约。
gap> x:=Indeterminate(GF(2));
x_1
gap> f := UnivariatePolynomial(GF(2), [1,1,1] );
#I Convert coefficient list to get compatibility with family
x_1^2+x_1+Z(2)^0
gap> L := SplittingField( f );
GF(2^2)
gap> IdGroup(GaloisGroup(AsField(GF(2),L)));
[ 2, 1 ]
n次分圆域是多项式x^n-1的分裂域,因此是有理数域的伽罗瓦扩域。
这个扩张的次数等于欧拉φ函数:[Q(ζ_n):Q]=φ(n)
Gal(Q(ζ_n)/Q)=(Z_n)^×——这个群是偶数阶交换群
gap> Phi(60);
16
gap> IdGroup(GaloisGroup(CyclotomicField(60)));
[ 16, 10 ]
正五边形的作图可能性在古希腊就已经知道了。
取a=ζ_5。
Gal(Q(ζ_5)/Q)=(Z/5Z)^×=F_5^×=C_4。
设E为x^8-1在Q上的分裂域。问[E:Q]=?并确定伽罗瓦群Gal(E/Q)。
取a=ζ_17。
Gal(Q(ζ_17)/Q)=(Z/17Z)^×=F_17^×=C_16。
gap> IdGroup(GaloisGroup(CF(5)));
[ 4, 1 ]
gap> IdGroup(GaloisGroup(CF(8)));
[ 4, 2 ]
gap> IdGroup(GaloisGroup(CF(15)));
[ 8, 2 ]
gap> IdGroup(GaloisGroup(CF(17)));
[ 16, 1 ]
U(8) ={[1]_8,[3]_8,[5]_8,[7]_8}=K_4≠C_4,
U(15)=U(3)×U(5)=C_2×C_4,
定理:n>=3且n≠6时,n次对称群的自同构都是内自同构,且Aut(S_n)=S_n。无限循环群的自同构群是C_2,C_n的自同构群是一个φ(n)阶群。
由于无限循环群有两个生成元,C_n有φ(n)个生成元,从而其自同构群分别为C_2和φ(n)阶群。令G与H是两个阶为互素的有限群,则Aut(G×H)=Aut(G)×Aut(H)。
gap> IdGroup(AutomorphismGroup(DihedralGroup(12)));
[ 12, 4 ]
gap> IdGroup(AutomorphismGroup(SmallGroup(12,5)));
[ 12, 4 ]
gap> IdGroup(DihedralGroup(12));
[ 12, 4 ]
gap> IdGroup(DirectProduct(SmallGroup(4,2),CyclicGroup(3)));
[ 12, 5 ]
gap> IdGroup(AutomorphismGroup(CyclicGroup(3)));
[ 2, 1 ]
Aut(C_3×C_2×C_2)=Aut(C_3)×Aut(C_2×C_2)=S_3×C_2=D_3×C_2=D_6
gap> IdGroup(AutomorphismGroup(CyclicGroup(2)));
[ 1, 1 ]
gap> IdGroup(AutomorphismGroup(CyclicGroup(6)));
[ 2, 1 ]
gap> Phi(6);
2
gap> IdGroup(AutomorphismGroup(Group((1,2,3,4,5))));
[ 4, 1 ]
gap> IdGroup(AutomorphismGroup(CyclicGroup(5)));
[ 4, 1 ]
gap> IdGroup(AutomorphismGroup(SmallGroup(4,2)));
[ 6, 1 ]
K_4有3个2阶群元,3个元素共有3!=6个排列,从而K_4有6个自同构。所以Aut(K_4)=S_3。
gap> IdGroup(AutomorphismGroup(QuaternionGroup(8)));
[ 24, 12 ]
??Aut(Q_8)=S_3,i,j,k的阶都是4
gap> IdGroup(AutomorphismGroup(SymmetricGroup(6)));
[ 1440, 5841 ]
gap> IdGroup(AutomorphismGroup(SymmetricGroup(5)));
[ 120, 34 ]
gap> IdGroup(AutomorphismGroup(SymmetricGroup(4)));
[ 24, 12 ]
gap> IdGroup(AutomorphismGroup(SymmetricGroup(3)));
[ 6, 1 ]
Aut(S_3)=S_3
gap> IdGroup(AutomorphismGroup(SymmetricGroup(2)));
[ 1, 1 ]
gap> IdGroup(AutomorphismGroup(SymmetricGroup(1)));
[ 1, 1 ]
gap> IdGroup(AutomorphismGroup(DihedralGroup(8)));
[ 8, 3 ]
Aut(D_4)=D_4
N阶导出群的例子:
(S_3)^(1)=A_3,(S_3)^(2)={1}=>S_3是可解群
(S_4)^(1)=A_4,(S_3)^(2)=V_4,(S_3)^(3)={1}=>S_4是可解群
gap> DerivedSeriesOfGroup(SmallGroup(6,1));
[ <pc group of size 6 with 2 generators>, Group([ f2 ]), Group([ ]) ]
gap> DerivedLength(SmallGroup(6,1));
2
gap> List(DerivedSeriesOfGroup(SmallGroup(6,1)),IdGroup);
[ [ 6, 1 ], [ 3, 1 ], [ 1, 1 ] ]
gap> List(DerivedSeriesOfGroup(SmallGroup(6,1)),Size);
[ 6, 3, 1 ]
gap> List(DerivedSeriesOfGroup(SymmetricGroup(4)),IdGroup);
[ [ 24, 12 ], [ 12, 3 ], [ 4, 2 ], [ 1, 1 ] ]
http://world.std/~jmccarro/math/SmallGroups/SmallGroups.html
注意:这个网站中的有限群编号与GAP4 ID不一致
群24.4=GAP4(24,1)
gap> IdGroup(Group((1,13,7,19,4,16,10,22)(2,15,8,21,5,18,11,24)(3,14,9,20,6,17,12,23), (1,7,4,10)(2,8,5,11)(3,9,6,12)(13,19,16,22)(14,20,17,23)(15,21,18,24), (1,4)(2,5)(3,6)(7,10)(8,11)(9,12)(13,16)(14,17)(15,18)(19,22)(20,23)(21,24), (1,2,3)(4,5,6)(7,8,9)(10,11,12)(13,14,15)(16,17,18)(19,20,21)(22,23,24)));
[ 24, 1 ]
gap> IdGroup(Center(SmallGroup(24,1)));
[ 4, 1 ]
群24.5=GAP4(24,3)
gap> IdGroup(Group((1,2)(3,4)(5,6)(7,8),(1,8,2,7)(3,6,4,5),(1,6,2,5)(3,7,4,8),(3,7,5)(4,8,6)));
[ 24, 3 ]
gap> IdGroup(Center(SmallGroup(24,3)));
[ 2, 1 ]
群24.6=GAP4(24,4)
gap> IdGroup(Group((1,13,4,16)(2,15,5,18)(3,14,6,17)(7,22,10,19)(8,24,11,21)(9,23,12,20), (1,7,4,10)(2,8,5,11)(3,9,6,12)(13,19,16,22)(14,20,17,23)(15,21,18,24), (1,4)(2,5)(3,6)(7,10)(8,11)(9,12)(13,16)(14,17)(15,18)(19,22)(20,23)(21,24), (1,2,3)(4,5,6)(7,8,9)(10,11,12)(13,14,15)(16,17,18)(19,20,21)(22,23,24)));
[ 24, 4 ]
gap> IdGroup(Center(SmallGroup(24,4)));
[ 2, 1 ]
群24.7=GAP4(24,5)
gap> IdGroup(Group((1,3,2)(4,6,5)(7,9,8)(10,12,11), (1,4)(2,5)(3,6)(7,10)(8,11)(9,12), (1,7,4,10)(2,8,5,11)(3,9,6,12), (2,3)(5,6)(8,9)(11,12)));
[ 24, 5 ]
gap> IdGroup(Center(SmallGroup(24,5)));
[ 4, 1 ]
群24.11=GAP4(24,10)
gap> IdGroup(Group((1,2)(3,4)(5,6), (1,7)(2,8)(3,9)(4,10)(5,11)(6,12), (1,3,5)(2,4,6)(7,9,11)(8,10,12), (7,8)(9,10)(11,12)));
[ 24, 10 ]
gap> IdGroup(Center(SmallGroup(24,10)));
[ 6, 2 ]
群24.12=GAP4(24,11)
gap> IdGroup(Group((1,13,2,14)(3,15,4,16)(5,17,6,18)(7,20,8,19)(9,22,10,21)(11,24,12,23), (1,7,2,8)(3,9,4,10)(5,11,6,12)(13,19,14,20)(15,21,16,22)(17,23,18,24), (1,3,5)(2,4,6)(7,9,11)(8,10,12)(13,15,17)(14,16,18)(19,21,23)(20,22,24), (1,2)(3,4)(5,6)(7,8)(9,10)(11,12)(13,14)(15,16)(17,18)(19,20)(21,22)(23,24)));
[ 24, 11 ]
gap> IdGroup(Center(SmallGroup(24,11)));
[ 6, 2 ]
群24.13=GAP4(24,12)
gap> IdGroup(Group((1,4)(2,3), (1,3)(2,4), (2,3), (2,3,4)));
[ 24, 12 ]
gap> IdGroup(Center(SmallGroup(24,12)));
[ 1, 1 ]
称辛群对它中心的商群Sp_n(F)/C为射影辛群,用PSp_n(F)表示。
定理:射影辛群PSp_n(F)是单群,除r=1,|F|=2或3和r=2,|F|=2,其中2r=n。
有限域F_q上辛群PSp_(2r)(F_q)的阶为:(q^(2r)-1)q^(2r-1)(q^(2r-2)-1)q^(2r-3)…(q^2-1)q。
Sp_4(F_2)=S_6(720阶群)。
gap> IdGroup(Sp(4,2));
[ 720, 763 ]
gap> IdGroup(SymmetricGroup(6));
[ 720, 763 ]
gap> IdGroup(PSp(4,2));
[ 720, 763 ]
定理:SL_2(K){<|}GL_2(K)。
SL_2(F_3)是一个24阶群2T,它有一个8阶的正规子群
gap> IdGroup(SL(2,3));
[ 24, 3 ]
PSL(2,2)=GL_2(F_2)=SL_2(F_2)=S_3
gap> IdGroup(PSL(2,2));
[ 6, 1 ]
gap> IdGroup(GL(2,2));
[ 6, 1 ]
gap> IdGroup(SL(2,2));
[ 6, 1 ]
称因子群SL_n(F)/C(SL_n(F))为射影特殊线性群,用PSL_n(F)表示。
定理:设n>=2,则除非n=2及F=F_2或F_3,PSL_n(K)是单群。
PSL(2,3)=T=A_4
gap> IdGroup(AlternatingGroup(4));
[ 12, 3 ]
gap> IdGroup(PSL(2,3));
[ 12, 3 ]
gap> IdGroup(GO(0,3,2));
[ 6, 1 ]
gap> IdGroup(GO(0,3,3));
[ 48, 48 ]
gap> IdGroup(GO(0,3,5));
[ 240, 189 ]
gap> IdGroup(GO(0,3,7));
[ 672, 1254 ]
gap> IdGroup(GO(-1,2,2));
[ 6, 1 ]
gap> IdGroup(GO(-1,2,3));
[ 8, 3 ]
gap> IdGroup(GO(-1,2,5));
[ 12, 4 ]
gap> IdGroup(GO(-1,2,7));
[ 16, 7 ]
gap> IdGroup(GO(-1,4,2));
[ 120, 34 ]
gap> IdGroup(GO(-1,4,3));
[ 1440, 5842 ]
gap> IdGroup(SpecialOrthogonalGroup(1,2,2));
[ 2, 1 ]
gap> IdGroup(SO(1,2,2));
[ 2, 1 ]
gap> IdGroup(GO(1,2,2));
[ 2, 1 ]
gap> IdGroup(GO(1,2,3));
[ 4, 2 ]
gap> IdGroup(GO(1,2,5));
[ 8, 3 ]
gap> IdGroup(GO(1,2,7));
[ 12, 4 ]
gap> IdGroup(GO(1,4,2));
[ 72, 40 ]
gap> IdGroup(GO(1,4,3));
[ 1152, 157478 ]
gap> Order(GO(1,4,4));
7200
1阶环即零环{0}
gap> NumberSmallRings(1);
1
gap> R:=SmallRing(1,1);
<ring with 1 generators>
gap> Elements(R);
[ 0*a ]
gap> GeneratorsOfRing(R);
[ a ]
gap> ShowAdditionTable(R);
+ | 0*a
----+----
0*a | 0*a
gap> ShowMultiplicationTable(R);
* | 0*a
----+----
0*a | 0*a
2阶环有2个:
gap> NumberSmallRings(2);
2
SmallRing(2,2)=GF(2)和SmallRing(2,1)=M_2=M_2(M_2^+=C_2)(称为加群为C_2的2阶零乘环),它们都是C_2的强抽象。
3阶环有2个:
gap> NumberSmallRings(3);
2
SmallRing(3,2)=GF(3)和SmallRing(3,1)=M_3=M_3(M_3^+=C_3)(称为加群为C_3的3阶零乘环)。
注意:同一个Abel群可以强抽象出不同构的多个环。Z_6的子环R={[0],[2],[4]}=Z_3=GF(3)与Z_9的子环S={[0],[3],[6]}=M_3=M_3(M_3^+=C_3)都是3阶循环环,但它们不同构。[作为加群同构但作为环不同构的有限循环环的例子]
5阶环有2个:
gap> NumberSmallRings(5);
2
SmallRing(5,2)=GF(5)和SmallRing(5,1)=M_5=M_5(M_5^+=C_5)(称为加群为C_5的5阶零乘环)
6阶环有4个:
gap> NumberSmallRings(6);
4
ring 6.Nu.1=M_6(M_6^+=C_6)={[0],[6],[12],[18],[24],[30]}
gap> R:=SmallRing(6,1);
<ring with 1 generators>
gap> ShowMultiplicationTable(R);
* | 0*a a 2*a 3*a 4*a -a
----+------------------------
0*a | 0*a 0*a 0*a 0*a 0*a 0*a
a | 0*a 0*a 0*a 0*a 0*a 0*a
2*a | 0*a 0*a 0*a 0*a 0*a 0*a
3*a | 0*a 0*a 0*a 0*a 0*a 0*a
4*a | 0*a 0*a 0*a 0*a 0*a 0*a
-a | 0*a 0*a 0*a 0*a 0*a 0*a
ring 6.Nu.2=R_2(R_2^+=C_6)={[0],[2],[4],[6],[8],[10]}
gap> R:=SmallRing(6,2);
<ring with 1 generators>
gap> ShowMultiplicationTable(R);
* | 0*a a 2*a 3*a 4*a -a
----+------------------------
0*a | 0*a 0*a 0*a 0*a 0*a 0*a
a | 0*a 4*a 2*a 0*a 4*a 2*a
2*a | 0*a 2*a 4*a 0*a 2*a 4*a
3*a | 0*a 0*a 0*a 0*a 0*a 0*a
4*a | 0*a 4*a 2*a 0*a 4*a 2*a
-a | 0*a 2*a 4*a 0*a 2*a 4*a
ring 6.Nu.3=R_3(R_3^+=C_6)={[0],[3],[6],[9],[12],[15]}
gap> R:=SmallRing(6,3);
<ring with 1 generators>
gap> ShowMultiplicationTable(R);
* | 0*a a 2*a 3*a 4*a -a
----+------------------------
0*a | 0*a 0*a 0*a 0*a 0*a 0*a
a | 0*a 3*a 0*a 3*a 0*a 3*a
2*a | 0*a 0*a 0*a 0*a 0*a 0*a
3*a | 0*a 3*a 0*a 3*a 0*a 3*a
4*a | 0*a 0*a 0*a 0*a 0*a 0*a
-a | 0*a 3*a 0*a 3*a 0*a 3*a
ring 6.u.1=Z_6={[0],[1],[2],[3],[4],[5]}
Z_2={[0],[1]}与Z_3={[0],[1],[2]}的外直和为Z_6,Z_6是其子环(也是理想)Z_2={[0],[3]}与Z_3={[0],[2],[4]}的内直和。在同构意义下,外直和与内直和二者是一致的。
gap> R:=SmallRing(6,4);
<ring with 1 generators>
gap> ShowMultiplicationTable(R);
* | 0*a a 2*a 3*a 4*a -a
----+------------------------
0*a | 0*a 0*a 0*a 0*a 0*a 0*a
a | 0*a a 2*a 3*a 4*a -a
2*a | 0*a 2*a 4*a 0*a 2*a 4*a
3*a | 0*a 3*a 0*a 3*a 0*a 3*a
4*a | 0*a 4*a 2*a 0*a 4*a 2*a
-a | 0*a -a 4*a 3*a 2*a a
定理:在所有的n阶循环环中,有而且只有T(n)(n的正因数个数)个是互不同构的。
C_n有而且只有T(n)个子群=>n阶循环环有而且只有T(n)个子环。
环Z_6=SmallRing(6,4)有T(6)=4个子环:{[0]},{[0],[3]},{[0],[2],[4]},Z_6
gap> S:=Subrings(SmallRing(6,4));
[ <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators> ]
gap> Size(S);
4
gap> List(S,GeneratorsOfRing);
[ [ 0*a ], [ 3*a ], [ 2*a ], [ a ] ]
gap> Elements(S[1]);
[ 0*a ]
gap> ShowMultiplicationTable(S[1]);
* | 0*a
----+----
0*a | 0*a
gap> ShowMultiplicationTable(S[2]);
* | 0*a 3*a
----+--------
0*a | 0*a 0*a
3*a | 0*a 3*a
gap> ShowMultiplicationTable(S[3]);
* | 0*a 2*a 4*a
----+------------
0*a | 0*a 0*a 0*a
2*a | 0*a 4*a 2*a
4*a | 0*a 2*a 4*a
gap> ShowMultiplicationTable(S[4]);
* | 0*a a 2*a 3*a 4*a -a
----+------------------------
0*a | 0*a 0*a 0*a 0*a 0*a 0*a
a | 0*a a 2*a 3*a 4*a -a
2*a | 0*a 2*a 4*a 0*a 2*a 4*a
3*a | 0*a 3*a 0*a 3*a 0*a 3*a
4*a | 0*a 4*a 2*a 0*a 4*a 2*a
-a | 0*a -a 4*a 3*a 2*a a
Z/6Z的全部理想有4个:Z_1,F_2,F_3,Z/6Z。
gap> I:=Ideals(SmallRing(6,4));
[ <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators> ]
gap> R:=SmallRing(6,4);I:=Ideals(R);
<ring with 1 generators>
[ <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators>, <ring with 1 generators> ]
gap> Q:=R/I[4];
<ring with 1 generators>
gap> ShowMultiplicationTable(Q);
* | 0*a
----+----
0*a | 0*a
gap> hom:= NaturalHomomorphismByIdeal(R,I[4]);
[ a ] -> [ 0*a ]
gap> Size(ImagesSource(hom));
1
gap> Size(R/I[3]);
3
gap> Size(R/I[2]);
2
gap> Size(R/I[1]);
6
gap> ShowMultiplicationTable(R/I[3]);
* | 0*q1 q1 -q1
-----+---------------
0*q1 | 0*q1 0*q1 0*q1
q1 | 0*q1 q1 -q1
-q1 | 0*q1 -q1 q1
1772年,欧拉发现了第8个梅森素数M8(10位数)。
gap> IsIrreducibleRingElement( Integers,2147483647);
true
gap> IsIrreducibleRingElement( Integers,2^31-1);
true
gap> IsPrime(Integers,2147483647);
true
gap> IsPrime(2147483647);
true
gap> IsPrime(GaussianIntegers,2147483647);
true
gap> IsPrime(GaussianIntegers,5);
false
gap> IsPrime(Integers,5);
true
gap> IsPrime(5);
true
gap> Factors(GaussianIntegers,5);
[ 2-E(4), 2+E(4) ]
gap> Factors(Integers,5);
[ 5 ]
gap> Factors(5);
[ 5 ]
gap> R:=PolynomialRing(Rationals,1);
Rationals[x_1]
gap> IsUniqueFactorizationRing(R);
true
gap> Units(GaussianIntegers);
[ -1, 1, -E(4), E(4) ]
gap> Units(Integers);
[ -1, 1 ]
gap> Units(ZmodnZ(4));
<group of size 2 with 1 generators>
gap> IdGroup(Units(ZmodnZ(4)));
[ 2, 1 ]
gap> IdGroup(Units(ZmodnZ(60)));
[ 16, 10 ]
gap> q:= QuaternionAlgebra( Rationals );
<algebra-with-one of dimension 4 over Rationals>
gap> IsField( q ); IsDivisionRing( q );
false
true
gap> IsDivisionRing(GaussianRationals);
true
gap> Algebra( Rationals, [Sqrt(-1)] );
<algebra over Rationals, with 1 generators>
gap> GaussianRationals=Algebra( Rationals, [Sqrt(-1)] );
true
gap> GaussianRationals=Algebra( Rationals, [Sqrt(-3)] );
false
gap> Algebra( Rationals, [Sqrt(-3)] );
<algebra over Rationals, with 1 generators>
gap> IsField(GF(2));
true
gap> IsUniqueFactorizationRing(GF(2));
false
gap> IsIntegralRing(GF(2));
true
gap> IsDivisionRing(GF(2));
true
gap> IsField(Ring(Sqrt(2)));
false
gap> IsRing(Ring(Sqrt(2)));
true
gap> IsRing(GF(2));
true
gap> IsRing(CF(1));
true
gap> IsRing(CF(3));
true
gap> Ring(1);
Integers
gap> IsRing(Integers);
true
gap> IsRing(Ring(1));
true
gap> IsField(Ring(1));
false
gap> IsIntegralRing(Integers);
true
gap> IsUniqueFactorizationRing(Ring(1));
true
gap> IsUniqueFactorizationRing(Integers);
true
gap> IsEuclideanRing(Integers);
true
gap> IsField(Ring(-1));
false
gap> IsRing(Ring(-1));
true
gap> Ring(-1);
<ring with 1 generators>
gap> IsUniqueFactorizationRing(Ring(-1));
false
gap> IsUniqueFactorizationRing(GaussianIntegers);
true
gap> IsUniqueFactorizationRing(DefaultRing(E(4)));
true
gap> IsUniqueFactorizationRing(Ring(E(4)));
false
gap> IsRing(Ring(E(4)));
true
gap> IsField(Ring(E(4)));
false
gap> DefaultRing(2,E(4));
GaussianIntegers
gap> DefaultRing(E(4));
GaussianIntegers
gap> IsRing(ZmodnZ(4));
true
gap> IsField(ZmodnZ(4));
false
gap> IsRing(ZmodnZ(5));
true
gap> IsField(ZmodnZ(5));
true
gap> IsField(Ring(CF(8)));
false
gap> IsRing(CF(8));
true
gap> IsRing(Ring(CF(8)));
true
gap> IsIntegralRing(CF(8));
true
两类不同的素域,从同构的意义上说任何域都可以看成有理数域Q的扩域或者p元域Fp的扩域
?p进域呢
定理:素域F只有以下两种:
(1)char F=0时F≌Q(有理数域),
(2)char F=p时F≌Fp。
R的特征为0,记为char R=0。
R的特征为p,记为char R=p。
素域与扩域的定义:设K是一个域,如果K的非空子集F在K的加法与乘法运算之下也成为一个域,则F称为K的子域,而K称为F的扩域。
一个域如果不包含更小的子域,则称为素域。因为若干个子域的交集还是一个子域,因此素域是存在的而且也是唯一的。
gap> IsPrimeField(GF(2));
true
gap> IsPrimeField(GaussianRationals);
false
gap> IsPrimeField(CF(4));
false
gap> CF(4);
GaussianRationals
gap> IsPrimeField(GF(3));
true
gap> IsPrimeField(GF(9));
false
gap> IsPrimeField(Rationals);
true
gap> IsPrimeField(CF(1));
true
gap> IsPrimeField(CF(2));
true
gap> CF(1);
Rationals
gap> CF(1)=CF(2);
true
有理数域是素域
gap> IsRing(Rationals);
true
gap> IsIntegralRing(Rationals);
true
gap> IsUniqueFactorizationRing(Rationals);
false
gap> IsField(Rationals);
true
Q是无限整环,是无限域
gap> IsPrimeField(Field(Sqrt(2)));
false
gap> IsPrimeField(Field(Sqrt(-2)));
false
gap> IsPrimeField(CF(3));
false
gap> KG := GroupRing( GF(3), DihedralGroup(16) );
<algebra-with-one over GF(3), with 4 generators>
gap> L := LieAlgebra ( KG );
#I LAGUNA package: Constructing Lie algebra ...
<Lie algebra over GF(3)>
gap> IsLieAlgebraByAssociativeAlgebra( L );
true
更多推荐
GAP软件的使用(20150514、20151002、20151004、20151012)







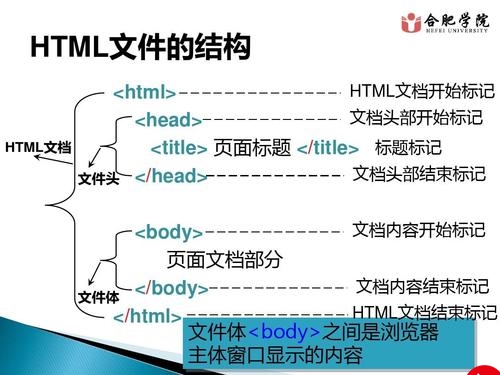
发布评论